题目内容
不等式|x|≥
的解集为
| 2 | x-1 |
{x|x<1或x≥2}
{x|x<1或x≥2}
.分析:讨论x的取值化简原不等式中的绝对值,当x大于等于0时,|x|=x,把原不等式进行变形,画出相应的图形,根据图形得出此时不等式的解集;当x小于0时,|x|=-x,把原不等式进行变形,判断得到化简后的分子恒大于0,商小于0,从而得到分母小于0,求出此时x的范围,得到原不等式的解集,综上,求出两种情况解集的并集即可得到原不等式的解集.
解答:解:若x≥0时,|x|=x,
原不等式变形为:x≥
,
整理得:
≥0,
在数轴上画出相应的图形,如图所示:
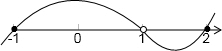
根据图形可得原不等式的解集为:-1≤x<1或x≥2;
若x<0时,|x|=-x,
原不等式变形得:-x≥
,
整理得:
≤0,
由x2-x+2恒大于0,得到x-1<0,解得x<1,
此时原不等式的解集为x<0,
综上,原不等式的解集为{x|x<1或x≥2}.
故答案为:{x|x<1或x≥2}
原不等式变形为:x≥
| 2 |
| x-1 |
整理得:
| (x-2)(x+1) |
| x-1 |
在数轴上画出相应的图形,如图所示:

根据图形可得原不等式的解集为:-1≤x<1或x≥2;
若x<0时,|x|=-x,
原不等式变形得:-x≥
| 2 |
| x-1 |
整理得:
| x2-x+2 |
| x-1 |
由x2-x+2恒大于0,得到x-1<0,解得x<1,
此时原不等式的解集为x<0,
综上,原不等式的解集为{x|x<1或x≥2}.
故答案为:{x|x<1或x≥2}
点评:此题考查了其他不等式的解法,利用分类讨论及数形结合的思想,是高考常考的题型.其思路为:根据绝对值的代数意义分x≥0和x<0两种情况分别化简原不等式,借助数轴及一元二次不等式的解法,得出原不等式的解集.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式
>0的解集是( )
| x-2 |
| x+3 |
| A、(-3,2) |
| B、(2,+∞) |
| C、(-∞,-3)∪(2,+∞) |
| D、(-∞,-2)∪(3,+∞) |
 A.(不等式选做题)不等式
A.(不等式选做题)不等式