题目内容
设 ,
, ,
, ,则( )
,则( )
A. | B. | C. | D. |
D
解析试题分析:一般地,只要涉及3个及以上的数比较大小,应找一中间量来比较,比如0、1.
由对数的性质知: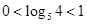 ,
,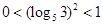 ,
,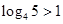 。又
。又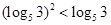 ,
,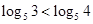
所以 .
.
解答本题目易进入作差比较的误区;其次是易弄错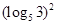 与
与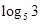 的大小.
的大小.
考点:对数函数的单调性及对数运算性质,以及比较数的大小的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 ,若
,若 ,则x的值是 ( )
,则x的值是 ( )
| A. | B.1或 | C.1,或± | D.1 |
已知 ,
, ,
, ,则( )
,则( )
| A.a>b>c | B.a>c>b | C.b>c>a | D.c>b>a |
如果函数 在区间
在区间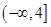 上是减函数,那么实数
上是减函数,那么实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
已知
 是(-∞,+∞)上的增函数,则a的取值范围是( ).
是(-∞,+∞)上的增函数,则a的取值范围是( ).
| A.(1,+∞) | B.(1,3) | C.[ ) ) | D.(1,  ) ) |
已知函数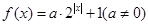 ,定义函数
,定义函数 给出下列命题:
给出下列命题:
① ; ②函数
; ②函数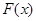 是奇函数;③当
是奇函数;③当 时,若
时,若 ,
, ,总有
,总有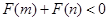 成立,其中所有正确命题的序号是( )
成立,其中所有正确命题的序号是( )
| A.② | B.①② | C.③ | D.②③ |
已知:
 则f(f(5))等于( )
则f(f(5))等于( )
| A.-1 | B.1 | C.-2 | D.2 |
设函数 则关于x的方程
则关于x的方程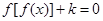 的根的情况,有下列说法:
的根的情况,有下列说法:
①存在实数k,使得方程恰有1个实数根
②存在实数k,使得方程恰有2个不相等的实数根
③存在实数k,使得方程恰有3个不相等的实数根
④存在实数k,使得方程恰有4个不相等的实数根
其中正确的是( )
| A.①③ | B.①② | C.②④ | D.③④ |
函数 的值域为( )
的值域为( )
| A.R | B. |
C. | D.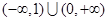 |