题目内容
设函数 则关于x的方程
则关于x的方程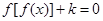 的根的情况,有下列说法:
的根的情况,有下列说法:
①存在实数k,使得方程恰有1个实数根
②存在实数k,使得方程恰有2个不相等的实数根
③存在实数k,使得方程恰有3个不相等的实数根
④存在实数k,使得方程恰有4个不相等的实数根
其中正确的是( )
| A.①③ | B.①② | C.②④ | D.③④ |
B
解析试题分析:因为 所以
所以 ,
,
当 时,
时,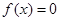 ,
, ,所以当
,所以当 时,关于x的方程
时,关于x的方程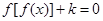 的恰有一个实根,则①正确.当
的恰有一个实根,则①正确.当 时,
时, ,所以当
,所以当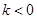 时,关于x的方程
时,关于x的方程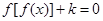 的恰有2个不相等实根,则②正确;③④错误.
的恰有2个不相等实根,则②正确;③④错误.
考点:分段函数,方程的根的判断.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
定义在R上的函数 满足
满足 且
且 ,
, ,则方程
,则方程 在区间
在区间 上的所有实根之和最接近下列哪个数( )
上的所有实根之和最接近下列哪个数( )
| A. 10 | B. 8 | C. 7 | D. 6 |
设 ,
, ,
, ,则( )
,则( )
A. | B. | C. | D. |
设 满足
满足 ,则
,则 =( )
=( )
A. | B.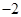 | C.1 | D. |
已知 ,则
,则 的大小关系是( )
的大小关系是( )
A.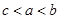 | B.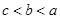 | C. | D. |
函数 由
由 确定,则方程
确定,则方程 的实数解有( )
的实数解有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
已知方程 的三个实根可分别作为一椭圆,一双曲线.一抛物线的离心率,则
的三个实根可分别作为一椭圆,一双曲线.一抛物线的离心率,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D.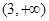 |
 和
和 (其中
(其中 ),
), 与函数
与函数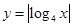 的图像从左至右相交于点
的图像从左至右相交于点 ,
, ,
, 与函数
与函数 ,
, .记线段
.记线段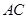 和
和 在
在 轴上的投影长度分别为
轴上的投影长度分别为 .当
.当 变化时,
变化时,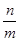 的最小值为( )
的最小值为( )



 的定义域为D,如果
的定义域为D,如果 ,使
,使 (C为常数
(C为常数 成立,则称函数
成立,则称函数 ;②
;② ;③
;③ ;④
;④ ,则满足在其定义域上均值为1的函数的个数是( )
,则满足在其定义域上均值为1的函数的个数是( )