题目内容
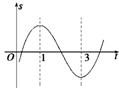 已知某质点的运动方程为s(t)=t3+bt2+ct+d,如图是其运动轨迹的一部分,若t∈[
已知某质点的运动方程为s(t)=t3+bt2+ct+d,如图是其运动轨迹的一部分,若t∈[| 1 | 2 |
分析:结合图象发现s(t)在t=1和t=3处取得极值,可建立两个等式,解出b与c的值,根据单调性求出s(t)在[
,4]上的最大值,使s(t)max<3d2,解出不等式即可.
| 1 |
| 2 |
解答: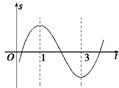 解:s'(t)=3t2+2bt+c.
解:s'(t)=3t2+2bt+c.
由图象可知,s(t)在t=1和t=3处取得极值.
则s'(1)=0,s'(3)=0.
即
解得
s'(t)=3t2-12t+9=3(t-1)(t-3).
当t∈[
,1)时,s'(t)>0.
当t∈(1,3)时,s'(t)<0.
当t∈(3,4)时,s'(t)>0.
则当t=1时,s(t)取得极大值为4+d.
又s(4)=4+d,
故t∈[
,4]时,s(t)的最大值为4+d.
已知s(t)<3d2在
,4]上恒成立,
∴s(t)max<3d2.即4+d<3d2.
解得d>
或d<-1.
∴d的取值范围是{d|d>
或d<-1}.
 解:s'(t)=3t2+2bt+c.
解:s'(t)=3t2+2bt+c.由图象可知,s(t)在t=1和t=3处取得极值.
则s'(1)=0,s'(3)=0.
即
|
|
s'(t)=3t2-12t+9=3(t-1)(t-3).
当t∈[
| 1 |
| 2 |
当t∈(1,3)时,s'(t)<0.
当t∈(3,4)时,s'(t)>0.
则当t=1时,s(t)取得极大值为4+d.
又s(4)=4+d,
故t∈[
| 1 |
| 2 |
已知s(t)<3d2在
| 1 |
| 2 |
∴s(t)max<3d2.即4+d<3d2.
解得d>
| 4 |
| 3 |
∴d的取值范围是{d|d>
| 4 |
| 3 |
点评:本题主要考查了利用导数研究函数的极值,以及函数恒成立问题等有关知识,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
如右图所示,定义在D上的函数f(x),如果满足:对?x∈D,常数A,都有f(x)≥A成立,则称函数f(x)在D上有下界,其中A称为函数的下界.(提示:图中的常数A可以是正数,也可以是负数或零)
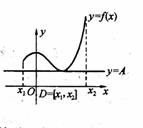 (本题满分12)如右图所示,定义在D上的函数
(本题满分12)如右图所示,定义在D上的函数