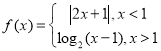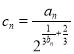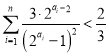题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)证明:![]() 的导函数
的导函数![]() 在区间
在区间![]() 上存在唯一零点;
上存在唯一零点;
(2)若对任意![]() ,均存在
,均存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
注:复合函数![]() 的导函数
的导函数![]() .
.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)设![]() ,则
,则![]() ,
,![]() .求出函数的导数,得到函数的单调区间,然后转化求解函数的零点.
.求出函数的导数,得到函数的单调区间,然后转化求解函数的零点.
(2)利用导数求出![]() 在区间
在区间![]() 上的最大值
上的最大值![]() ,
,![]() 在区间
在区间![]() 上的最大值
上的最大值![]() ,通过
,通过![]() 求实数
求实数![]() 的取值范围.
的取值范围.
解:(Ⅰ)设![]() ,则
,则![]() ,
,
![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
又![]() ,
,![]() ,
,![]() ,
,
故![]() 在区间
在区间![]() 上存在唯一零点.
上存在唯一零点.
(Ⅱ)记![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,
,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
依题意,“对任意![]() ,均存在
,均存在![]() ,使得
,使得![]() ”等价于“
”等价于“![]() ”.
”.
由(Ⅰ)知,![]() 在
在![]() 只有一个零点,设为
只有一个零点,设为![]() ,
,
且当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
又![]() ,
,![]() ,所以当
,所以当![]() 时,
时,![]() .
.
故应满足![]() .
.
因为![]() ,所以
,所以![]() .
.
①当![]() 时,
时,![]() ,对任意
,对任意![]() ,
,![]() ,不满足
,不满足![]() .
.
②当![]() 时,令
时,令![]() ,得
,得![]() 或
或![]() .
.
(i)当![]() ,即
,即![]() 时,在
时,在![]() 上,
上,![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,![]() .
.
由![]() ,得
,得![]() ,所以
,所以![]() .
.
(ii)当![]() ,即
,即![]() 时,在
时,在![]() 上,
上,![]() ,
,![]() 单调递增;在
单调递增;在![]() 上,
上,![]() ,
,![]() 单调递减.
单调递减.![]() .
.
由![]() ,得
,得![]() 或
或![]() ,所以
,所以![]() .
.
(iii)当![]() ,即
,即![]() 时,显然在
时,显然在![]() 上,
上,![]() ,
,![]() 单调递增,于是
单调递增,于是![]() ,此时不满足
,此时不满足![]() .
.
综上,实数![]() 的取值范围是
的取值范围是![]() .
.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案【题目】学生考试中答对但得不了满分的原因多为答题不规范,具体表现为:解题结果正确,无明显推理错误,但语言不规范、缺少必要文字说明、卷面字迹不清、得分要点缺失等,记此类解答为“![]() 类解答”.为评估此类解答导致的失分情况,某市教研室做了一项试验:从某次考试的数学试卷中随机抽取若干属于“
类解答”.为评估此类解答导致的失分情况,某市教研室做了一项试验:从某次考试的数学试卷中随机抽取若干属于“![]() 类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
类解答”的题目,扫描后由近百名数学老师集体评阅,统计发现,满分12分的题,阅卷老师所评分数及各分数所占比例大约如下表:
教师评分(满分12分) | 11 | 10 | 9 |
各分数所占比例 |
|
|
|
某次数学考试试卷评阅采用“双评+仲裁”的方式,规则如下:两名老师独立评分,称为一评和二评,当两者所评分数之差的绝对值小于等于1分时,取两者平均分为该题得分;当两者所评分数之差的绝对值大于1分时,再由第三位老师评分,称之为仲裁,取仲裁分数和一、二评中与之接近的分数的平均分为该题得分;当一、二评分数和仲裁分数差值的绝对值相同时,取仲裁分数和前两评中较高的分数的平均分为该题得分.(假设本次考试阅卷老师对满分为12分的题目中的“![]() 类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
类解答”所评分数及比例均如上表所示,比例视为概率,且一、二评与仲裁三位老师评分互不影响).
(1)本次数学考试中甲同学某题(满分12分)的解答属于“![]() 类解答”,求甲同学此题得分
类解答”,求甲同学此题得分![]() 的分布列及数学期望
的分布列及数学期望![]() ;
;
(2)本次数学考试有6个解答题,每题满分均为12分,同学乙6个题的解答均为“![]() 类解答”,记该同学6个题中得分为
类解答”,记该同学6个题中得分为![]() 的题目个数为
的题目个数为![]() ,
,![]() ,
,![]() ,计算事件“
,计算事件“![]() ”的概率.
”的概率.