题目内容
9．已知函数f（x）=$\frac{1}{{3}^{x}+2}$，则函数在（0，+∞）上（ ）| A． | 单调递减且无最小值 | B． | 单调递减且有最小值 | ||
| C． | 单调递增且无最大值 | D． | 单调递增且有最大值 |
分析 根据复合函数单调性之间的关系进行判断即可．
解答 解：∵y=3x+2在（0，+∞）是为增函数，且y＞2，
∴f（x）=$\frac{1}{{3}^{x}+2}$在（0，+∞）上为减函数，则0＜y＜$\frac{1}{2}$，
则函数在（0，+∞）上为减函数，无最大值和无最小值，
故选：A
点评 本题主要考查函数单调性的判断，根据复合函数单调性之间的关系是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
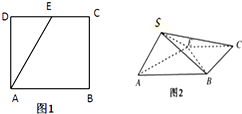如图，点E为正方形ABCD边CD上异于点C，D的动点，将△ADE沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列三个说法中正确的个数是（ ）
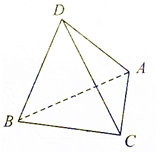如图，A、B、C、D为空间四点，△ABC中，AB=AC=BC=2，等边三角形ADB以AB为轴运动，当平面ADB⊥平面ABC时，则CD=$\sqrt{6}$．