题目内容
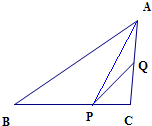
在△ABC中,点P在BC上,且
=2
,Q是AC的中点,以P为坐标原点建立平面直角坐标系,若
=(4,3),
=(1,5),则
=( )
| BP |
| PC |
| PA |
| PQ |
| BC |
| A.(6,-21) | B.(2,-7) | C.(-2,-7) | D.(-6,21) |
设C坐标为(x,y),
∵P为坐标原点,∴
=(x,y),
∵△PAC中,Q为AC中点,∴
=
(
+
),
结合
=(4,3),
=(1,5),可得
,解之得x=-2,y=7.
∴
=(-2,7),可得
=2
=(-4,14),
因此,
=
+
=(-6,21),
故选:D
∵P为坐标原点,∴
| PC |
∵△PAC中,Q为AC中点,∴
| PQ |
| 1 |
| 2 |
| PA |
| PC |
结合
| PA |
| PQ |
|
∴
| PC |
| BP |
| PC |
因此,
| BC |
| BP |
| PC |
故选:D


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
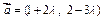 与
与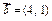 共线,则
共线,则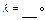
 =(
=( ,
, )(其中
)(其中 )平移,就是将图形F()
)平移,就是将图形F() ,
, ,
, ,有下列四个命题:
,有下列四个命题: ,
,
 ,使得
,使得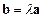 ;
; ,则
,则 或
或 ;
; ,
, 使得
使得 ;
; ,则
,则 .
. ,则B
,则B 分
分 所成的比为( )
所成的比为( )

