题目内容
气象部门提供了某地今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t (单位:℃) | t 22℃ 22℃ | 22℃< t 28℃ 28℃ | 28℃< t  32℃ 32℃ | 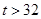 ℃ ℃ |
| 天数 | 6 | 12 |  |  |
 和
和 数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.
数据不清楚,但气象部门提供的资料显示,六月份的日最高气温不高于32℃的频率为0.9.(Ⅰ) 若把频率看作概率,求
 ,
, 的值;
的值;(Ⅱ) 把日最高气温高于32℃称为本地区的 “高温天气”,根据已知条件完成下面
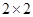 列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.
列联表,并据此你是否有95%的把握认为本地区的“高温天气”与西瓜“旺销”有关?说明理由.| | 高温天气 | 非高温天气 | 合计 |
| 旺销 | 1 | | |
| 不旺销 | | 6 | |
| 合计 | | | |

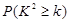 | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(Ⅰ)9,3;(Ⅱ)没有95%的把握认为本地区的“高温天气”与西瓜 “旺销”有关.
解析试题分析:(Ⅰ)把频率看作概率, 学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”. 小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数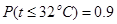 ,根据频率和为1,可求得
,根据频率和为1,可求得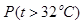 ,在由皮书等于频率
,在由皮书等于频率 样本总数,便求得
样本总数,便求得 ,
,  的值;(Ⅱ)利用
的值;(Ⅱ)利用 求出
求出 的观测值,把
的观测值,把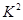 的值与临界值比较,如下表:确定
的值与临界值比较,如下表:确定 与
与 有关系的程度或无关系.
有关系的程度或无关系.
若P(k2>k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828  ,则有95℅的把握说明两个事件有关;
,则有95℅的把握说明两个事件有关;
若 ,则有99℅的把握说明两个事件有关;
,则有99℅的把握说明两个事件有关;
若 ,则没有理由认为两个事件有关.
,则没有理由认为两个事件有关.
试题解析:(Ⅰ)由已知的: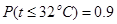 ,
,
∴  ,
,
∴ 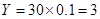 ,
,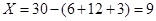 . 6分
. 6分
(Ⅱ) 高温天气 非高温天气 合 计 旺销<

创新大课堂系列丛书寒假作业系列答案
创新自主学习寒假新天地系列答案
创优教学寒假作业年度总复习系列答案
导学练寒假作业云南教育出版社系列答案
第三学期寒假衔接系列答案
骄子之路寒假作业河北人民出版社系列答案
冬之卷快乐假日系列答案
动力源期末寒假作业系列答案
非常完美完美假期寒假作业系列答案
新浪书业复习总动员学期总复习寒系列答案
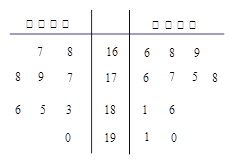
(Ⅰ)用分层抽样的方法从“高个子”和“非高个子”中抽取5人,如果从这5人中随机选2人,那么至少有1人是“高个子”的概率是多少?男 女 8 16 5 8 9 8 7 6 17 2 3 5 5 6 7 4 2 18 0 1 2 1 19 0
(Ⅱ)若从所有“高个子”中随机选3名志愿者,用 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
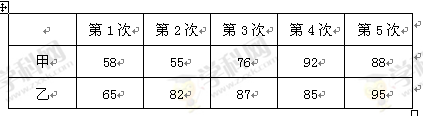
的数学期望.  及天数如下表:
及天数如下表:
试依据以频率估计概率的统计思想,解答下列问题:售出个数 
10 11 12 13 14 15 天数 3 3 3 6 9 6
(Ⅰ)计算小王某天售出该现烤面包超过13个的概率;
(Ⅱ)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量. 试求小王增加订购量的概率.
(Ⅲ)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
 ,求随机变量
,求随机变量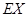 .
. .
.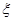 ,试写出
,试写出 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是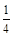 .
. 表示回答该题正确的人数,求
表示回答该题正确的人数,求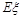 .
.
 饮料,另外2杯为
饮料,另外2杯为 饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯
饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯