题目内容
(本小题满分14分)
已知向量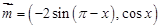 ,
,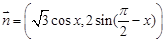 ,函数
,函数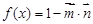 .
.
(1)求函数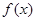 的解析式;
的解析式;
(2)当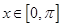 时,求
时,求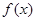 的单调递增区间;
的单调递增区间;
(3)说明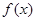 的图象可以由
的图象可以由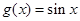 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到.
已知向量
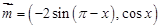 ,
,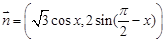 ,函数
,函数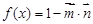 .
.(1)求函数
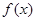 的解析式;
的解析式;(2)当
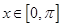 时,求
时,求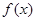 的单调递增区间;
的单调递增区间;(3)说明
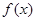 的图象可以由
的图象可以由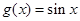 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到. (1) 
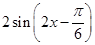 ;
;
(2) 和
和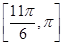 ;(3)见解析
;(3)见解析

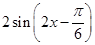 ;
;(2)
 和
和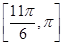 ;(3)见解析
;(3)见解析(1)先利用向量的数量积的坐标表示求出f(x)的表达式
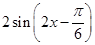 .
.
(2)在(1)的基础上利用正弦函数的单调增区间来求f(x)的增区间即可.
(3)根据平移的左加右减的规则以及伸缩规则可知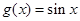 经过怎么样的变换得到
经过怎么样的变换得到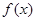
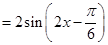 的图象.
的图象.
解:(1)∵m•n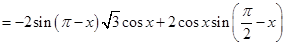
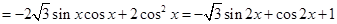 …………………………2分
…………………………2分
∴ 1
1 m•n
m•n ,……………………3分
,……………………3分
∴
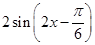 .………………………4分
.………………………4分
(2)由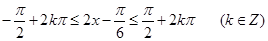 ,
,
解得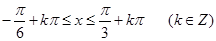 ,……………………6分
,……………………6分
∵取k=0和1且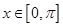 ,得
,得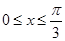 和
和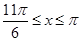 ,
,
∴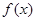 的单调递增区间为
的单调递增区间为 和
和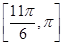 .……………………………8分
.……………………………8分
法二:∵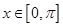 ,∴
,∴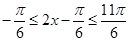 ,
,
∴由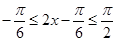 和
和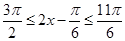 , ………………………6分
, ………………………6分
解得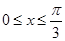 和
和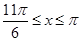 ,
,
∴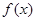 的单调递增区间为
的单调递增区间为 和
和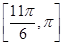 .………………8分
.………………8分
(3)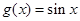 的图象可以经过下面三步变换得到
的图象可以经过下面三步变换得到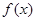
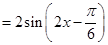 的图象:
的图象:
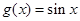 的图象向右平移
的图象向右平移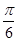 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的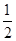 倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到
倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到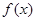
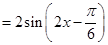 的图象.………………………14分(每一步变换2分)
的图象.………………………14分(每一步变换2分)

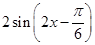 .
.(2)在(1)的基础上利用正弦函数的单调增区间来求f(x)的增区间即可.
(3)根据平移的左加右减的规则以及伸缩规则可知
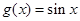 经过怎么样的变换得到
经过怎么样的变换得到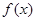
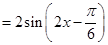 的图象.
的图象.解:(1)∵m•n
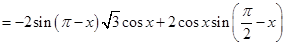
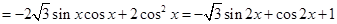 …………………………2分
…………………………2分∴
 1
1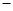 m•n
m•n ,……………………3分
,……………………3分∴

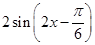 .………………………4分
.………………………4分(2)由
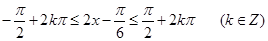 ,
,解得
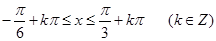 ,……………………6分
,……………………6分∵取k=0和1且
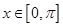 ,得
,得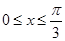 和
和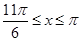 ,
,∴
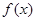 的单调递增区间为
的单调递增区间为 和
和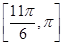 .……………………………8分
.……………………………8分法二:∵
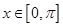 ,∴
,∴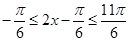 ,
,∴由
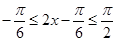 和
和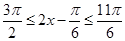 , ………………………6分
, ………………………6分解得
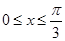 和
和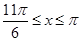 ,
,∴
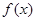 的单调递增区间为
的单调递增区间为 和
和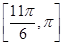 .………………8分
.………………8分(3)
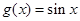 的图象可以经过下面三步变换得到
的图象可以经过下面三步变换得到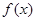
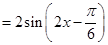 的图象:
的图象: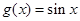 的图象向右平移
的图象向右平移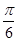 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的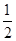 倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到
倍(纵坐标不变),最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),得到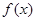
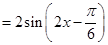 的图象.………………………14分(每一步变换2分)
的图象.………………………14分(每一步变换2分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )的部分图象.
)的部分图象. =
= ,0<α<
,0<α< ,求cosα的值.
,求cosα的值.
 (
( ,
, )为偶函数,且函数
)为偶函数,且函数 图象的两相邻对称轴间的距离为
图象的两相邻对称轴间的距离为 .
. 的值;
的值; 个单位后,得到函数
个单位后,得到函数 的图象,求
的图象,求 的单调递减区间.
的单调递减区间.  的一部分图象如图,那么
的一部分图象如图,那么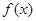 的解析式以及
的解析式以及
 的值分别是( )
的值分别是( )
 ,
, 
 ,
, 
 ,
,  ,
,  的最大值是3,则它的最小值_____________
的最大值是3,则它的最小值_____________  在抛物线
在抛物线 上,点
上,点 在圆
在圆 上,
上, 的最小值为( )
的最小值为( )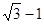



 为奇函数,该函数的部分图 像如图所示,
为奇函数,该函数的部分图 像如图所示,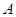 、
、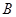 分别为最高点与最低点,且
分别为最高点与最低点,且
 ,则该函数图象的一条对称轴为( )
,则该函数图象的一条对称轴为( )




 (
( )的图象如右图所示,为了得到
)的图象如右图所示,为了得到 的图象,可以将
的图象,可以将 的图象( )
的图象( )
 个单位长度
个单位长度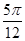 个单位长度
个单位长度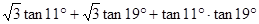 的值是( ).
的值是( ).