题目内容
(09年临沭县模块考试文)(14分)
已知圆M的方程为:![]() 及定点N(3,0),动点P在圆M上运动,线
及定点N(3,0),动点P在圆M上运动,线
段PN的垂直平分线交圆M的半径MP于点Q,设点Q的轨迹为曲线C。
(Ⅰ)求曲线C的方程;
(Ⅱ)试问:过点![]() 是否存在直线l,使直线l与曲线C交于A,B两点,且
是否存在直线l,使直线l与曲线C交于A,B两点,且
![]() ,(O为坐标原点)。若存在,求出直线l的方程;若不存在,说明理
,(O为坐标原点)。若存在,求出直线l的方程;若不存在,说明理
由。
解析:(Ⅰ)|MP|=|MQ|+|QP|
又∵Q在PN的垂直平分线上,
∴|QP|=|QN|,
∴|MP|=|QM|+|QN|,
即|QM|+|QN|=10
∴曲线C是焦点为M、N的椭圆,c=3,a=5,b=4.
∴曲线C方程为![]() ?????????????????6分
?????????????????6分
(Ⅱ)假设存在这样的直线l,当斜率l不存在使,A、O、B共线,不满足条件。
设l的斜率为k,![]()
∴l的方程为![]() ????????????????8分
????????????????8分
由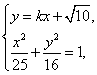
得![]()
∴![]() ?????????????????10分
?????????????????10分
![]()
![]()
又∵![]()
代入得![]()
∴![]() ?????????????????13分
?????????????????13分
∴假设成立,这样的直线存在,方程为![]() ?????????????????14分
?????????????????14分

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
 且{Cn}的前n项和为Tn,求T2n(n∈N*)。
且{Cn}的前n项和为Tn,求T2n(n∈N*)。