Question

【题目】已知椭圆E：（a＞b＞0）的离心率e.

（1）若点P（1，）在椭圆E上，求椭圆E的标准方程；

（2）若D（2，0）在椭圆内部，过点D斜率为的直线交椭圆E于M.N两点，|MD|＝2|ND|，求椭圆E的方程.

Answer 1

【答案】（1）（2）

【解析】

（1）因为，所以，则，所以，将P（1，）代入方程，得b2＝1，所以a2＝4，可得椭圆方程；

（2）设M（x1，y1），N（x2，y2），设y1＜y2，因为，所以椭圆的方程为，MN的直线方程为x2，联立求解韦达定理，结合条件|MD|＝2|ND|，可得y1＝﹣2y2，所以解得，，代入根与系数关系，得b2＝3，a2＝12，求得椭圆E的方程.

（1）因为，所以，则，所以，

将P（1，）代入方程，得b2＝1，所以a2＝4，

所以椭圆E的标准方程为；

（2）设M（x1，y1），N（x2，y2），不妨设y1＜y2，

因为，所以椭圆的方程为，MN的直线方程为x2，

联立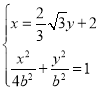，得，16y2+8y+12﹣12b2＝0，

所以y1+y2，y1y2①.

因为|MD|＝2|ND|，即y1＝﹣2y2，所以，，

代入①，得b2＝3，a2＝12，

所以椭圆E的方程为.