题目内容
设函数f(x)=ax2+bx+clnx,(其中a,b,c为实常数且a>0),曲线y=f(x)在点(1,f(1))处的切线方程为y=3x-3,
(Ⅰ)若函数f(x)无极值点且f′(x)存在零点,求a,b,c的值;
(Ⅱ)若函数f(x)有两个极值点,证明f(x)的极小值小于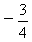 。
。
(Ⅰ)若函数f(x)无极值点且f′(x)存在零点,求a,b,c的值;
(Ⅱ)若函数f(x)有两个极值点,证明f(x)的极小值小于
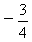 。
。解:(Ⅰ)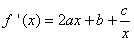 ,
,
由题得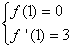 ,即
,即
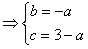 ,
,
此时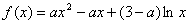 ,
,
 ;
;
由f(x)无极值点且f′(x)存在零点,
得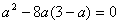
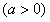 ,
,
解得 ,
,
于是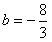 ,
,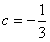 ;
;
(Ⅱ)由(Ⅰ)知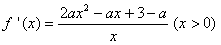 ,
,
要使函数f(x)有两个极值点,
只要方程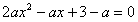 有两个不等正根,
有两个不等正根,
那么实数a应满足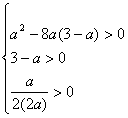 ,解得
,解得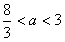 ,
,
设两正根为 ,且
,且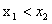 ,
,
可知当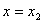 时有极小值
时有极小值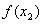 ,
,
其中这里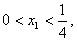
由于对称轴为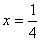 ,所以
,所以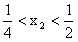 ,
,
且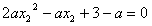 ,得
,得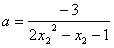 ,
,
记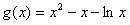 ,
,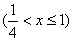 ,
,
有 对
对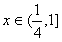 恒成立,
恒成立,
又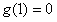 ,故对
,故对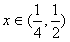 恒有
恒有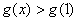 ,即
,即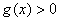 ,
,
所以有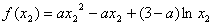
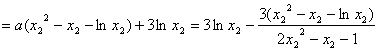
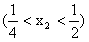
而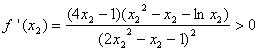 对于
对于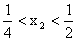 恒成立,
恒成立,
即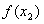 在
在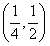 上单调递增,
上单调递增,
故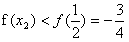 。
。
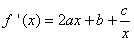 ,
,由题得
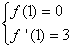 ,即
,即
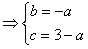 ,
,此时
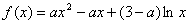 ,
, ;
;由f(x)无极值点且f′(x)存在零点,
得
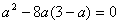
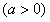 ,
,解得
 ,
,于是
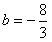 ,
,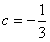 ;
;(Ⅱ)由(Ⅰ)知
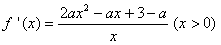 ,
,要使函数f(x)有两个极值点,
只要方程
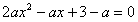 有两个不等正根,
有两个不等正根,那么实数a应满足
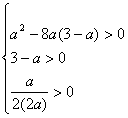 ,解得
,解得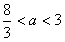 ,
,设两正根为
 ,且
,且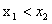 ,
,可知当
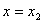 时有极小值
时有极小值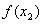 ,
,其中这里
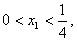
由于对称轴为
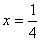 ,所以
,所以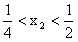 ,
,且
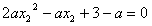 ,得
,得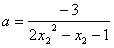 ,
,记
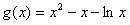 ,
,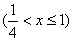 ,
,有
 对
对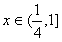 恒成立,
恒成立,又
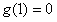 ,故对
,故对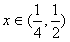 恒有
恒有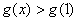 ,即
,即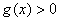 ,
,所以有
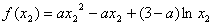
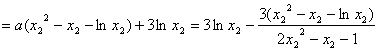
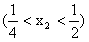
而
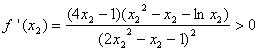 对于
对于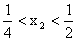 恒成立,
恒成立,即
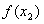 在
在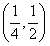 上单调递增,
上单调递增,故
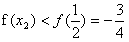 。
。
练习册系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |