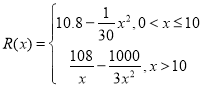题目内容
【题目】已知数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,均有
,均有![]() (
(![]() 是常数,且
是常数,且![]() )成立,则称数列
)成立,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为“
为“![]() 数列”,求数列
数列”,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)若数列![]() 为“
为“![]() 数列”,且
数列”,且![]() 为整数,试问:是否存在数列
为整数,试问:是否存在数列![]() ,使得
,使得![]() 对任意
对任意![]() ,
,![]() 成立?如果存在,求出这样数列
成立?如果存在,求出这样数列![]() 的
的![]() 的所有可能值,如果不存在,请说明理由.
的所有可能值,如果不存在,请说明理由.
【答案】(1)![]() (2)存在,
(2)存在,![]()
【解析】
![]() 由数列
由数列![]() 为“
为“![]() 数列”可得,
数列”可得,![]() ,
,![]() ,两式相减得
,两式相减得![]() ,又
,又![]()
![]() ,利用等比数列通项公式即可求出
,利用等比数列通项公式即可求出![]() ,进而求出
,进而求出![]() ;
;
![]() 由题意得,
由题意得,![]() ,
,![]() ,两式相减得,
,两式相减得,![]() ,
,
据此可得,当![]() 时,
时,![]() ,进而可得
,进而可得![]() ,即数列
,即数列![]() 为常数列,进而可得
为常数列,进而可得![]() ,结合
,结合![]() ,得到关于
,得到关于![]() 的不等式,再由
的不等式,再由![]() 时
时![]() ,且
,且![]() 为整数即可求出符合题意的
为整数即可求出符合题意的![]() 的所有值.
的所有值.
![]() 因为数列
因为数列![]() 为“
为“![]() 数列”,
数列”,
所以![]() ,故
,故![]() ,
,
两式相减得![]() ,
,
在![]() 中令
中令![]() ,则可得
,则可得![]() ,故
,故![]()
所以![]() ,
,
所以数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列,
为公比的等比数列,
所以![]() ,因为
,因为![]() ,
,
所以![]() .
.
(2)由题意得![]() ,故
,故![]() ,
,
两式相减得![]()
所以,当![]() 时,
时,![]()
又因为![]()
所以当![]() 时,
时,![]()
所以![]() 成立,
成立,
所以当![]() 时,数列
时,数列![]() 是常数列,
是常数列,
所以![]()
因为当![]() 时,
时,![]() 成立,
成立,
所以![]() ,
,
所以![]()
在![]() 中令
中令![]() ,
,
因为![]() ,所以可得
,所以可得![]() ,
,
所以![]() ,
,
由![]() 时
时![]() ,且
,且![]() 为整数,
为整数,
可得![]() ,
,
把![]() 分别代入不等式
分别代入不等式![]()
可得,![]() ,
,
所以存在数列![]() 符合题意,
符合题意,![]() 的所有值为
的所有值为![]() .
.

【题目】某市正在进行创建全国文明城市的复验工作,为了解市民对“创建全国文明城市”的知识知晓程度,某权威调查机构对市民进行随机调查,并对调查结果进行统计,共分为优秀和一般两类,先从结果中随机抽取100份,统计得出如下![]() 列联表:
列联表:
优秀 | 一般 | 总计 | |
男 | 25 | 25 | 50 |
女 | 30 | 20 | 50 |
总计 | 55 | 45 | 100 |
(1)根据上述列联表,是否有![]() 的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
(2)现从调查结果为一般的市民中,按分层抽样的方法从中抽取9人,然后再从这9人中随机抽取3人,求这三位市民中男女都有的概率;
(3)以样本估计总体,视样本频率为概率,从全市市民中随机抽取10人,用![]() 表示这10人中优秀的人数,求随机变量
表示这10人中优秀的人数,求随机变量![]() 的期望和方差.
的期望和方差.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
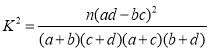 (其中
(其中![]() ).
).
【题目】在“互联网+”时代的今天,移动互联快速发展,智能手机(Smartphone)技术不断成熟,尤其在5G领域,华为更以![]() 件专利数排名世界第一,打破了以往由美、英、日垄断的前三位置,再次荣耀世界,而华为的价格却不断下降,远低于苹果;智能手机成为了生活中必不可少的工具,学生是对新事物和新潮流反应最快的一个群体之一,越来越多的学生在学校里使用手机,为了解手机在学生中的使用情况,对某学校高二年级
件专利数排名世界第一,打破了以往由美、英、日垄断的前三位置,再次荣耀世界,而华为的价格却不断下降,远低于苹果;智能手机成为了生活中必不可少的工具,学生是对新事物和新潮流反应最快的一个群体之一,越来越多的学生在学校里使用手机,为了解手机在学生中的使用情况,对某学校高二年级![]() 名同学使用手机的情况进行调查,针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如下的数据:
名同学使用手机的情况进行调查,针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如下的数据:
使用时间(小时) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
所占比例 | 4% | 10% | 31% | 16% |
| 12% | 2% |
(1)求表中![]() 的值;
的值;
(2)从该学校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于![]() 小时的概率?若能,请算出这个概率;若不能,请说明理由;
小时的概率?若能,请算出这个概率;若不能,请说明理由;
(3)若从使用手机![]() 小时和
小时和![]() 小时的两组中任取两人,调查问卷,看看他们对使用手机进行娱乐活动的看法,求这
小时的两组中任取两人,调查问卷,看看他们对使用手机进行娱乐活动的看法,求这![]() 人都使用
人都使用![]() 小时的概率.
小时的概率.