题目内容
若不等式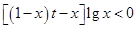
对任意正整数
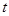恒成立，则实数
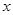的取值范围是（ ）
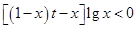对任意正整数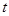恒成立，则实数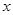的取值范围是（ ）A． | B． | C． | D． |
C
分析：因为有因式lgx，所以须对x分x＞1，0＜x＜1和x=1三种情况讨论，在每一种情况下求出对应的x的范围，最后综合即可．
解答：解：由题知x＞0，所以当x＞1时，lgx＞0，
不等式[（1-x）n-x]lgx＜0转化为（1-x）n-x＜0?a＞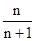
=1-
对任意正整数n恒成立?x＞1．
当0＜x＜1时，lgx＜0，
不等式[（1-x）n-x]lgx＜0转化为（1-x）n-x＞0?x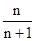＜=1-对任意正整数n恒成立?x＜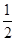
，
∵0＜x＜1，∴0＜x＜．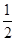
当x=1时，lgx=0，不等式不成立舍去
综上，实数x的取值范围是 x＞1或0＜x＜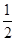
故选C．
解答：解：由题知x＞0，所以当x＞1时，lgx＞0，
不等式[（1-x）n-x]lgx＜0转化为（1-x）n-x＜0?a＞
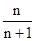=1-对任意正整数n恒成立?x＞1．当0＜x＜1时，lgx＜0，
不等式[（1-x）n-x]lgx＜0转化为（1-x）n-x＞0?x＜
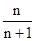=1-对任意正整数n恒成立?x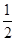＜，∵0＜x＜1，∴0＜x＜
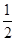．当x=1时，lgx=0，不等式不成立舍去
综上，实数x的取值范围是 x＞1或0＜x＜
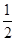
故选C．
练习册系列答案
相关题目
。
的不等式
在
上恒成立，则
的取值范围是 。
，
，则下列关系式中正确的是 ( )
B 
C 
D 
对任意
都成立，则
的取值范围为 （ ）
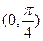
，则有 （ ）
