题目内容
在区间[0,1]上任意取两个实数a,b,则函数f(x) =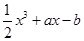 在区间[-1,1]上有且仅有一个零点的概率为
在区间[-1,1]上有且仅有一个零点的概率为
A.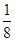 | B. | C.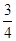 | D.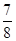 |
D
解析
试题分析:∵ ,∴
,∴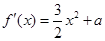 ,∵
,∵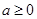 ,∴
,∴ ,∴函数f(x) =
,∴函数f(x) =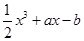 在区间[-1,1]上单调递增,若函数f(x) =
在区间[-1,1]上单调递增,若函数f(x) =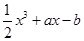 在区间[-1,1]上有且仅有一个零点,则f(-1)×f(1)<0,化简得
在区间[-1,1]上有且仅有一个零点,则f(-1)×f(1)<0,化简得 ,即
,即 ,故根据题意作出(a,b)满足的区域面积为1,符合条件的区域(如图阴影部分)的面积为1-
,故根据题意作出(a,b)满足的区域面积为1,符合条件的区域(如图阴影部分)的面积为1- ,则所求的概率为
,则所求的概率为 ,故选D
,故选D
考点:本题考查了几何概型概率的求法
点评:若一次试验中所有可能结果和某个事件A包含的结果(基本事件)都对应一个长度,如线段长、时间区间、距离、路程等,那么需要求出各自相应的长度,然后运用几何概型的计算公式即可求出事件A发生的概率

练习册系列答案
相关题目
已知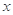 、
、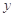 满足约束条件
满足约束条件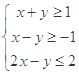 , 若目标函数
, 若目标函数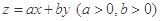 的最大值为7, 则
的最大值为7, 则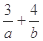 的最小值为( )
的最小值为( )
| A.14 | B.7 | C.18 | D.13 |
已知变量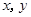 满足约束条件
满足约束条件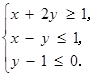 则
则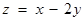 的最大值为
的最大值为
A.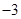 | B. | C. | D.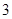 |
设变量x,y满足约束条件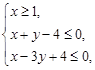 则目标函数z=3x-y的最大值为
则目标函数z=3x-y的最大值为
A.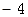 | B.0 | C. | D.4 |
设 为坐标原点,
为坐标原点, ,若
,若 满足
满足 ,则
,则 的最大值为
的最大值为
| A.4 | B.6 | C.8 | D.10 |
点 满足平面区域:
满足平面区域: ,点
,点 满足:
满足: ,则
,则 的最小值是( )
的最小值是( )
A. | B. | C. | D. |
动点 在区域
在区域 上运动,则
上运动,则 的范围( )。
的范围( )。
A. | B. |
C. | D. |
若直线y=2x上存在点(x,y)满足 则实数m的最大值为 ( )
则实数m的最大值为 ( )
| A.-1 | B.1 | C. | D.2 |
设变量x,y满足约束条件: .则目标函数z=2x+3y的最小值为( )
.则目标函数z=2x+3y的最小值为( )
| A.6 | B.7 | C.8 | D.23 |