题目内容
【题目】对正整数n，设曲线y=xn（1﹣x）在x=2处的切线与y轴交点的纵坐标为an ， 则数列 
的前n项和的公式是（ ）
A.2n
B.2n﹣2
C.2n+1
D.2n+1﹣2
【答案】D
【解析】解：∵y'|x=2=﹣2n﹣1（n+2）， ∴切线方程为：y+2n=﹣2n﹣1（n+2）（x﹣2），
令x=0，求出切线与y轴交点的纵坐标为y0=（n+1）2n ，
所以 
，则数列 
的前n项和 
【考点精析】通过灵活运用导数的几何意义和数列的前n项和，掌握通过图像,我们可以看出当点
趋近于
时，直线
与曲线相切．容易知道，割线
的斜率是
，当点趋近于时，函数
在
处的导数就是切线PT的斜率k，即
；数列{an}的前n项和sn与通项an的关系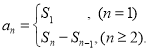
即可以解答此题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】已知两个函数f（x）和g（x）的定义域和值域都是集合{1，2，3}，其定义如下表：则方程g（f（x））=x的解集为（ ）
x | 1 | 2 | 3 |
f（x） | 2 | 3 | 1 |
x | 1 | 2 | 3 |
g（x） | 3 | 2 | 1 |
A.{1}
B.{2}
C.{3}
D.
