题目内容
【题目】定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为“三角形”数列,对于“三角形”数列
为“三角形”数列,对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”
的“保三角形函数”![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() 是数列
是数列![]() 的“保三角形函数”,求k的取值范围;
的“保三角形函数”,求k的取值范围;
(2)已知数列![]() 的首项为2010,
的首项为2010,![]() 是数列
是数列![]() 的前n项和,且满足
的前n项和,且满足![]() ,证明
,证明![]() 是“三角形”数列.
是“三角形”数列.
【答案】(1)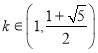 (2)见解析
(2)见解析
【解析】
(1)由题得![]() ,解不等式即得解;
,解不等式即得解;
(2)先求出![]() ,再证明
,再证明![]()
![]() .
.
(1)显然![]() 对任意正整数都成立,
对任意正整数都成立,
即![]() 是三角形数列.
是三角形数列.
因为![]() ,显然有
,显然有![]() ,
,
由![]() 得
得![]() ,
,
解得![]() .因为
.因为![]() ,
,
所以当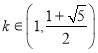 时,
时,![]() 是数列
是数列![]() 的“保三角形函数”.
的“保三角形函数”.
(2)由![]() 得
得![]() ,
,
两式相减得![]() .
.
所以![]() ,因为
,因为![]()
所以![]() ,所以数列
,所以数列![]() 是等比数列.
是等比数列.
所以![]() .
.
显然![]() ,
,
因为![]()
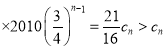 ,
,
所以![]() 是“三角形”数列.
是“三角形”数列.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目