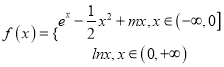题目内容
【题目】为了解学生身高情况,某校以![]() 的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为
的比例对全校1000名学生按性别进行分层抽样调查,已知男女比例为![]() ,测得男生身高情况的频率分布直方图(如图所示):
,测得男生身高情况的频率分布直方图(如图所示):
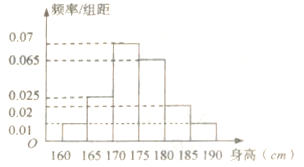
(1)计算所抽取的男生人数,并估计男生身高的中位数(保留两位小数);
(2)从样本中身高在![]() 之间的男生中任选2人,求至少有1人身高在
之间的男生中任选2人,求至少有1人身高在![]() 之间的概率.
之间的概率.
【答案】(1)174.64cm(2)![]() .
.
【解析】试题分析:
(1)由题意结合中位数的求法可得男生身高的中位数是174.64cm;
(2)列出所有可能的事件,结合古典概型公式可得至少有1人身高在![]() 之间的概率是
之间的概率是![]() .
.
试题解析:
(1)由题意得,所抽取的男生人数为:
1000×8%×![]() =40人
=40人
依据样本频率分布直方图:0.01×5+0.025×5+x=0.5 得x=0.325 ,而身高170~175之间的频率为0.35,所以中位数为170+5×![]() ≈174.64cm
≈174.64cm
(2)样本中身高在180~185 cm之间的男生有4人,设其编号为①,②,③,④,样本中身高在185~190 cm之间的男生有2人,设其编号为⑤,⑥,从上述6人中任取2人的共有:
(①,②)(①,③)(①,④)(①,⑤)(①,⑥)
(②,③)(②,④)(②,⑤)(②,⑥)
(③,④)(③,⑤)(③,⑥)
(④,⑤)(④,⑥)
(⑤,⑥)
故从样本中身高在180~190 cm之间的男生中任选2人的所有可能结果数为15,至少有1人身高在185~190 cm之间的可能结果数为9,因此,所求概率P2=![]() =
=![]() .
.

 口算能手系列答案
口算能手系列答案【题目】某工厂的甲、乙两个车间的![]() 名工人进行了劳动技能大比拼,规定:技能成绩大于或等于
名工人进行了劳动技能大比拼,规定:技能成绩大于或等于![]() 分为优秀,
分为优秀, ![]() 分以下为非优秀,统计成成绩后,得到如下的
分以下为非优秀,统计成成绩后,得到如下的![]() 列联表,且已知在甲、乙两个车间工人中随机抽取
列联表,且已知在甲、乙两个车间工人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲车间 |
| ||
乙车间 |
| ||
合计 |
|
(1)请完成上面的列联表;
(2)根据列联表的数据,若按![]() 的可靠性要求,能否认为“成绩与车间有关系”?
的可靠性要求,能否认为“成绩与车间有关系”?