题目内容
已知函数
(1)求函数 单调递增区间;
单调递增区间;
(2)若存在 ,使得
,使得 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围.

(1)求函数
 单调递增区间;
单调递增区间;(2)若存在
 ,使得
,使得 是自然对数的底数),求实数
是自然对数的底数),求实数 的取值范围.
的取值范围.(1)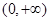 ;(2)
;(2)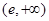
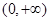 ;(2)
;(2)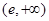
试题分析:(1)求导函数
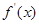 ,解不等式
,解不等式 ,其解集和定义域求交集,得函数的单调递增区间,该题中
,其解集和定义域求交集,得函数的单调递增区间,该题中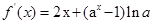
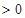 ,不等式不易解出,但是可观察到当
,不等式不易解出,但是可观察到当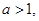 且
且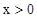 时
时 恒成立,故函数在整个定义域内单调递增;(2)由题知只需
恒成立,故函数在整个定义域内单调递增;(2)由题知只需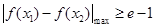 ,即
,即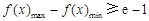
问题转化为求函数
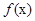 在
在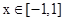 的值域问题,观察得
的值域问题,观察得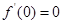 ,当
,当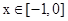 时,
时,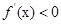 ;当
;当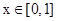 时,
时,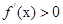 ,则
,则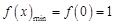 ,最大值为
,最大值为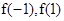 中的较大者,进而得关于
中的较大者,进而得关于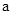 的不等式,再考虑不等式的解集即为实数
的不等式,再考虑不等式的解集即为实数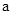 的取值范围.
的取值范围.试题解析:⑴
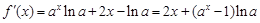 .
.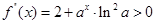 ,所以
,所以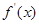 在
在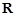 上是增函数,
上是增函数, 又
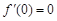 ,所以不等式
,所以不等式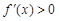 的解集为
的解集为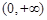 ,
,故函数
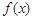 的单调增区间为
的单调增区间为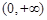
⑶因为存在
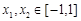 ,使得
,使得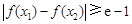 成立,
成立,而当
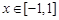 时,
时,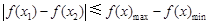 ,
,所以只要
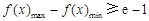 即可.
即可. 又因为
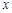 ,
,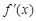 ,
,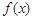 的变化情况如下表所示:
的变化情况如下表所示: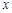 | 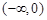 |  | 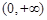 |
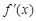 | 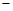 |  |  |
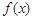 | 减函数 | 极小值 | 增函数 |
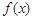 在
在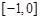 上是减函数,在
上是减函数,在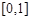 上是增函数,所以当
上是增函数,所以当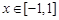 时,
时,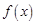 的最小值
的最小值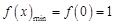 ,
,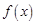 的最大值
的最大值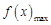 为
为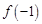 和
和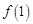 中的最大值.
中的最大值.因为
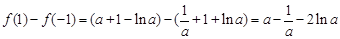 ,
,令
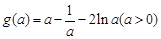 ,因为
,因为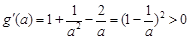 ,
,所以
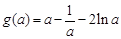 在
在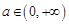 上是增函数.
上是增函数.而
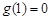 ,故当
,故当 时,
时,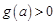 ,即
,即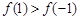 ;
;所以,当
 时,
时,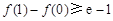 ,即
,即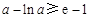 ,函数
,函数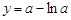 在
在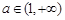 上是增函数,解得
上是增函数,解得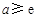 ;
;
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
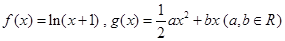 .
.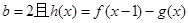 存在单调递减区间,求实数
存在单调递减区间,求实数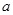 的取值范围;
的取值范围; ,求证:当
,求证:当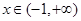 时,
时,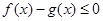 恒成立;
恒成立;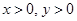 ,则
,则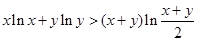 .
. .
. 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围; 上的最小值为3,求实数
上的最小值为3,求实数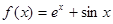 ,
,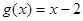 ;
;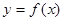 在
在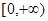 上单调递增;
上单调递增;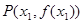 ,
,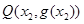
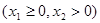 ,若直线
,若直线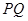
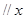 轴,求
轴,求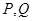 两点间的最短距离.
两点间的最短距离. 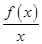 .
.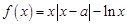 ,
,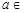
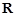 .
.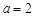 ,求函数
,求函数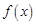 在区间
在区间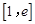 上的最值;
上的最值;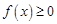 恒成立,求
恒成立,求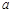 的取值范围. 注:
的取值范围. 注: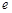 是自然对数的底数.
是自然对数的底数.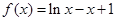 ,
,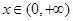 ,
,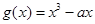 .
.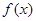 的最大值;
的最大值;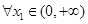 ,总存在
,总存在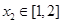 使得
使得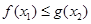 成立,求
成立,求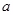 的取值范围;
的取值范围;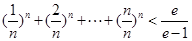 .
.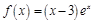 的单调递增区间是( )
的单调递增区间是( )