题目内容
设函数 (
( )
)
(Ⅰ)若函数 是定义在R上的偶函数,求a的值;
是定义在R上的偶函数,求a的值;
(Ⅱ)若不等式 对任意
对任意 ,
, 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
(Ⅰ)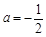 ;(Ⅱ)
;(Ⅱ)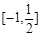 .
.
【解析】
试题分析:(Ⅰ)函数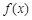 是定义在R上的偶函数,则
是定义在R上的偶函数,则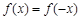 恒成立,代入解析式得:
恒成立,代入解析式得:
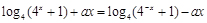 ,
,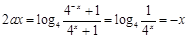 .即
.即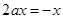 对任意
对任意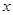 都成立,由此得
都成立,由此得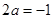 ,
,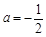 .(Ⅱ)不等式
.(Ⅱ)不等式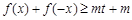 对任意
对任意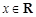 ,恒成立,则
,恒成立,则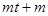 小于等于
小于等于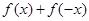 的最大值,而
的最大值,而
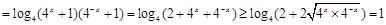 .所以
.所以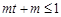 对任意
对任意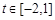 恒成立,
恒成立,
令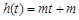 ,这是关于
,这是关于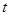 的一次函数,故只需
的一次函数,故只需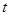 取两个端点的值时不等式成立即可,即
取两个端点的值时不等式成立即可,即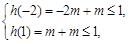 ,解之即可得实数m的取值范围.
,解之即可得实数m的取值范围.
试题解析:(Ⅰ)由函数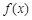 是定义在R上的偶函数,则
是定义在R上的偶函数,则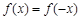 恒成立,
恒成立,
即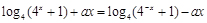 ,所以
,所以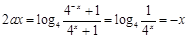 ,
,
所以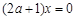 恒成立,则
恒成立,则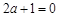 ,故
,故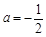 . 4分
. 4分
(Ⅱ)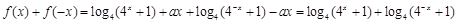
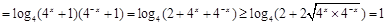 .
.
所以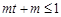 对任意
对任意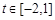 恒成立,令
恒成立,令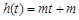 ,
,
由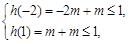 解得
解得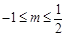 ,
,
故实数m的取值范围是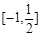 . 12分
. 12分
考点:1、函数的奇偶性;2、不等式恒成立问题.

练习册系列答案
相关题目