题目内容
如图所示,直三棱柱ABC A1B1C1中,D,E分别是AB,BB1的中点.
A1B1C1中,D,E分别是AB,BB1的中点.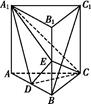
(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2 ,求三棱锥C
,求三棱锥C A1DE的体积.
A1DE的体积.
(1)见解析 (2)1
解析(1)证明:连接AC1交A1C于点F,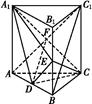
则F为AC1中点.
又D是AB中点,连接DF,
则BC1∥DF.
因为DF?平面A1CD,BC1?平面A1CD,
所以BC1∥平面A1CD.
(2)解:因为ABC A1B1C1是直三棱柱,
A1B1C1是直三棱柱,
所以AA1⊥CD.
由已知AC=CB,D为AB的中点,
所以CD⊥AB.
又AA1∩AB=A,
于是CD⊥平面ABB1A1.
由AA1=AC=CB=2,AB=2
得∠ACB=90°,CD= ,A1D=
,A1D= ,DE=
,DE= ,A1E=3,
,A1E=3,
故A1D2+DE2=A1E2,
即DE⊥A1D.
所以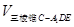 =
=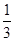 ×
×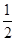 ×
× ×
× ×
× ="1."
="1."

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 中,底面
中,底面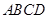 是边长为
是边长为 的正方形,
的正方形,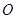 为
为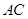 与
与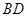 的交点,
的交点,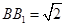 ,
,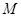 是线段
是线段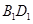 的中点.
的中点.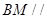 平面
平面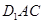 ;
;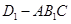 的体积.
的体积.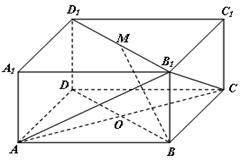
 中,
中,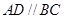 ,
,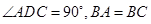 .把
.把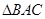 沿
沿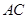 折起到
折起到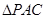 的位置,使得
的位置,使得 点在平面
点在平面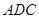 上的正投影
上的正投影 恰好落在线段
恰好落在线段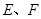 分别为棱
分别为棱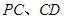 的中点.
的中点.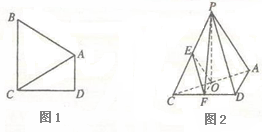
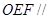 平面
平面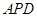 ;
;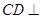 平面
平面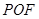 ;
; ,求四棱锥
,求四棱锥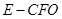 的体积.
的体积.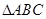 是边长为6的等边三角形,
是边长为6的等边三角形,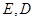 分别为
分别为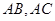 靠近
靠近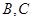 的三等分点,点
的三等分点,点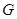 为边
为边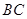 边的中点,线段
边的中点,线段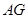 交线段
交线段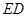 于点
于点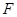 .将
.将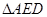 沿
沿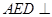 平面
平面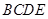 ,连接
,连接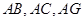 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.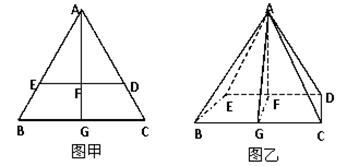
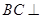 平面
平面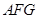
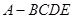 的体积.
的体积.  所在的平面和平面
所在的平面和平面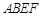 互相垂直,等腰梯形
互相垂直,等腰梯形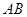 ∥
∥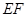 ,
,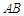 =2,
=2,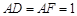 ,
,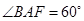 ,
,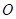 ,
, 分别为
分别为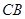 的中点,
的中点,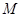 为底面
为底面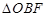 的重心.
的重心.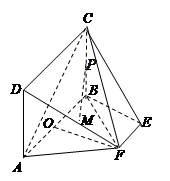
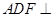 平面
平面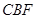 ;
;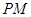 ∥平面
∥平面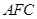 ;
; 的体积
的体积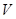 .
. 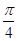 ,∠DAB=
,∠DAB=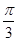 .沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题:
.沿直径AB折起,使两个半圆所在的平面互相垂直(如图乙),F为BC的中点,E为AO的中点.根据图乙解答下列各题: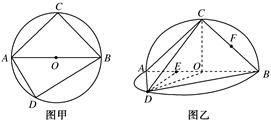
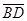 上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.
上是否存在一点G,使得FG∥平面ACD?若存在,试确定点G的位置;若不存在,请说明理由.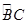 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).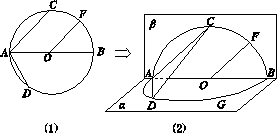
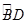 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.