题目内容
已知-| π |
| 3 |
| π |
| 6 |
| 6m-1 |
| 6m+5 |
分析:根据x的范围,利用余弦函数的图象求出cosx的范围,即得到
的范围,列出关于m的不等式,求出不等式的解集即可得到m的取值范围.
| 6m-1 |
| 6m+5 |
解答:解:∵-
≤x≤
,
∴
≤cosx≤1,
∴
≤
≤1,
即(
-
)(
-1)≤0,
∴
•
≤0,
∴6m-7≥0,即m≥
.
故答案为:m≥
| π |
| 3 |
| π |
| 6 |
∴
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 6m-1 |
| 6m+5 |
即(
| 6m-1 |
| 6m+5 |
| 1 |
| 2 |
| 6m-1 |
| 6m+5 |
∴
| 6m-7 |
| 2(6m+5) |
| -6 |
| 6m+5 |
∴6m-7≥0,即m≥
| 7 |
| 6 |
故答案为:m≥
| 7 |
| 6 |
点评:此题考查了其他不等式的解法,考查转化的数学思想,是一道综合题.

练习册系列答案
相关题目
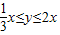 ,则x+y的最大值为 ,最小值为 .
,则x+y的最大值为 ,最小值为 .