题目内容

已知3≤x≤6，
13
x≤y≤2x，则x+y的最大值为
18
18
，最小值为
4
4
．
分析：利用线性规划的有关知识即可得出．
解答：解：如图所示，令x+y=t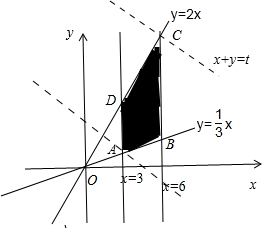，得直线l：y=-x+t．
联立
x=3
y=
1
3
x
解得A（3，1）；
联立
x=6
y=2x
，解得C（6，12）．
则当直线l过点A（3，1）时，t=3+1取得最小值4；
当直线l过点C（6，12）时，t=6+12=18取得最大值18．
故答案分别为18，4．
点评：熟练掌握线性规划夹角最值问题是解题的关键．
练习册系列答案
相关题目
已知f(x)=
x2
1+x 2
，那么f(2)+f(
1
2
)+f(3)+f(
1
3
)+f(4)+f(
1
4
)+f(5)+(
1
5
)+f(6)+f(
1
6
)=
5
5
．
已知cos（x+
π
6
）=
1
3
，（0＜x＜
π
2
）则cosx=
3
+2
2
6
3
+2
2
6
．
已知cos（x-
π
6
）=
1
3
，则 cos（
5π
6
+x）+sin（
π
3
+x）=
0
0
．
已知sin(x+
π
3
)=
1
3
，则sin(
2π
3
-x)+sin2(
π
6
-x)=
11
9
11
9
．
已知sin(x-
π
3
)=
1
3
，则cos(x+
π
6
)=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网