题目内容
已知正方体ABCD-A1B1C1D1的棱长为2,P、Q分别是BC、CD上的动点,且|PQ|=![]() ,建立如下图所示的坐标系;确定P、Q的位置,使得B1Q⊥D1P.
,建立如下图所示的坐标系;确定P、Q的位置,使得B1Q⊥D1P.

答案:
解析:
解析:
|
解:如图,设BP=t,则CQ=
DQ=2- ∴ ∵B1Q⊥D1P等价于 即-2 即 此时,P、Q分别是棱BC、CD的中点,即当P、Q分别是棱BC、CD的中点时,B1Q⊥D1P. |

练习册系列答案
相关题目
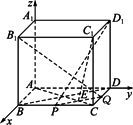
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1= 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.