题目内容
【题目】已知函数
.
（1）求函数
在
上的最小值
的表达式；
（2）若函数在上有且只有一个零点，求
的取值范围.
【答案】（1）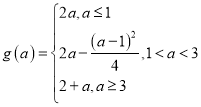
；（2）
.
【解析】
（1）求出函数
的对称轴方程，对实数
分
、
、
三种情况讨论，分析函数在区间
上的单调性，进而可得出函数在区间上的最小值
的表达式；
（2）对函数分情况讨论：（i）方程
在区间上有两个相等的实根；（ii）①方程在区间
只有一根；（②
；③
.可得出关于实数的等式或不等式，即可解得实数的取值范围.
（1）
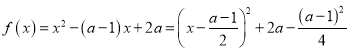，其对称轴为
，
当，即
时，函数在区间上单调递减，
；
当，即
时，函数在区间
上单调递减，在区间
上单调递增，
；
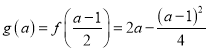当时，即当
时，函数在区间上单调递增，
.
综上所述：；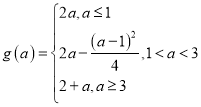
（2）（i）若方程
在上有两个相等的实数根，
则
，此时无解；
（ii）若方程有两个不相等的实数根.
①当只有一根在内时，
，即
，得
；
②当时，
，方程化为
，其根为
，
，满足题意；
③当时，
，方程化为
，其根为
，
，满足题意.
综上所述，的取值范围是.
【题目】某种产品的质量以其“无故障使用时间
(单位：小时)”衡量，无故障使用时间越大表明产品质量越好，且无故障使用时间大于3小时的产品为优质品，从某企业生产的这种产品中抽取100件，并记录了每件产品的无故障使用时间，得到下面试验结果：
无故障使用时间 |
|
|
|
频数 | 20 | 40 | 40 |
以试验结果中无故障使用时间落入各组的频率作为一件产品的无故障使用时间落入相应组的概率.
(1)从该企业任取两件这种产品，求至少有一件是优质品的概率；
(2)若该企业生产的这种产品每件销售利润
(单位：元)与其无故障使用时间
的关系式为
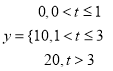
从该企业任取两件这种产品，其利润记为
(单位：元)，求
的分布列与数学期望.
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关, 现收集了该种药用昆虫的6组观测数据如下表：
温度x/C | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得： 
， 
， 
， 
，
，线性回归模型的残差平方和
，e8.0605≈3167，其中xi, yi分别为观测数据中的温度和产卵数，i=1, 2, 3, 4, 5, 6.
(Ⅰ)若用线性回归模型，求y关于x的回归方程
=
x+
（精确到0.1）；
(Ⅱ)若用非线性回归模型求得y关于x的回归方程为
=0.06e0.2303x，且相关指数R2=0.9522.
( i )试与(Ⅰ)中的回归模型相比，用R2说明哪种模型的拟合效果更好.
( ii )用拟合效果好的模型预测温度为35C时该种药用昆虫的产卵数（结果取整数）.
附：一组数据(x1,y1), (x2,y2), ...,(xn,yn ), 其回归直线
=
x+
的斜率和截距的最小二乘估计为
=
；相关指数R2=
．
