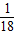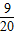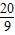题目内容
．若随机变量η的分布列如下：
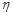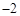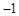 |  |  | 0 | 1 | 2 | 3 |
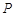 | 0.1 | 0.2 | 0.2 | 0.3 | 0.1 | 0.1 |
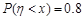时，实数x的取值范围是（ ）Ａ．x≤2 Ｂ．1≤x≤2 Ｃ．1＜x≤2 Ｄ．1＜x＜2
C
解析试题分析：由随机变量的性质，随机变量的概率之和等于1.因为P(-2)+P(-1)+P(0)+P(1)0.8，所以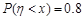时，1＜x≤2，故选C。
考点：本题主要考查随机变量分布列的性质。
点评：简单题，分布列中，随机变量的概率之和等于1.
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
若随机变量X的分布列如下表，则E（X）=（ ）
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 2x | 3x | 7x | 2x | 3x | x |
A、
| ||
B、
| ||
C、
| ||
D、
|
某城市出租汽车的起步价为10元，行驶路程不超出4km时租车费为10元，若行驶路程超出4km，则按每超出lkm加收2元计费（超出不足lkm的部分按lkm计）．从这个城市的民航机场到某宾馆的路程为15km．某司机经常驾车在机场与此宾馆之间接送旅客，由于行车路线的不同以及途中停车时间要转换成行车路程（这个城市规定，每停车5分钟按lkm路程计费），这个司机一次接送旅客的行车路程X是一个随机变量．设他所收租车费为η．
（1）求租车费η关于行车路程X的关系式；
（2）若随机变量X的分布列为
求所收租车费η的数学期望．
（3）已知某旅客实付租车费38元，而出租汽车实际行驶了15km，问出租车在途中因故停车累计最多几分钟？
（1）求租车费η关于行车路程X的关系式；
（2）若随机变量X的分布列为
| X | 15 | 16 | 17 | 18 |
| P | 0.1 | 0.5 | 0.3 | 0.1 |
（3）已知某旅客实付租车费38元，而出租汽车实际行驶了15km，问出租车在途中因故停车累计最多几分钟？