题目内容
一批产品共100件,其中有10件是次品,为了检验其质量,从中以随机的方式选取5件,求在抽取的这5件产品中次品数分布列与期望值,并说明5件中有3件以上(包括3件)为次品的概率.(精确到0.001)
0.07
抽取的次品数是一个随机变量,设为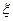 ,显然
,显然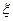 可以取从0到5的6个整数.
可以取从0到5的6个整数.
抽样中,如果恰巧有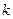 个(
个(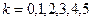 )次品,则其概率为
)次品,则其概率为
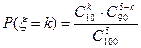
按照这个公式计算,并要求精确到0.001,则有
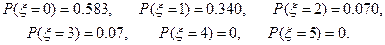
故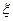 的分布列为
的分布列为
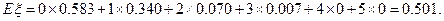
由分布列可知,
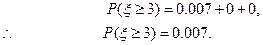
这就是说,所抽取的5件品中3件以上为次品的可能性很小,只有7%.
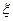 ,显然
,显然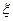 可以取从0到5的6个整数.
可以取从0到5的6个整数.抽样中,如果恰巧有
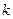 个(
个(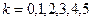 )次品,则其概率为
)次品,则其概率为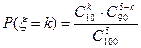
按照这个公式计算,并要求精确到0.001,则有
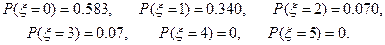
故
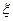 的分布列为
的分布列为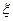 | 0 | 1 | 2 | 3 | 4 | 5 |
| P | 0.583 | 0.340 | 0.070 | 0.007 | 0 | 0 |
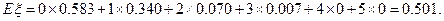
由分布列可知,
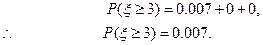
这就是说,所抽取的5件品中3件以上为次品的可能性很小,只有7%.

练习册系列答案
相关题目
 和
和 ,现已知目标被命中,则它是甲命中的概率是多少?
,现已知目标被命中,则它是甲命中的概率是多少? 则该单位员工总数为 ( )
则该单位员工总数为 ( ) 在第一次抽取时被抽到的概率是多少?
在第一次抽取时被抽到的概率是多少? (元)间的每位同学得助学金1500元,家庭收入在
(元)间的每位同学得助学金1500元,家庭收入在 (元)间的每位同学得助学金1000元,家庭收入在
(元)间的每位同学得助学金1000元,家庭收入在 (元),间的同学不发助学金,记该年级某位同学所得助学金为
(元),间的同学不发助学金,记该年级某位同学所得助学金为 元,写出
元,写出 元,求
元,求

 上随机取一个数x,
上随机取一个数x, 的值介于0到
的值介于0到 之间的概率为( ).
之间的概率为( ).



