题目内容
已知函数
f(x)=x
2+ax+2blnx
(1)若b=1时,函数f(x)在(0,1)上不单调,求实数a的取值范围;
(2)若函数在(0,m)和(n,+∞)上为增函数,在(m,n)上为减函数(其中0<m<1,1<n<2).求b-a的取值范围.
分析:(1)先求导函数,由于函数f(x)在(0,1)上不单调的情况不好讨论,要使函数f(x)在区间上是单调函数,则导数≤0或≥0恒成立,列出不等式求出解集即可到得到a的取值范围;
(2)由函数的单调区间,得到导函数为0的解为m,n,再依据0<m<1,1<n<2,得到有关a,b的不等式,得到可行域,由线性规划问题,得到b-a的取值范围.
解答:解:(1)由已知
f′(x)=x+a+,若函数f(x)在(0,1)上单调,
则
x+a+≥0恒成立,或
x+a+≤0恒成立,
由
x+a+≥0(0<x<1)恒成立等价于
x+≥-a,
令
μ(x)=x+,则μ(x)在(0,1)上为减函数,所以μ(x)>μ(1)=3,则3≥-a,即a≥-3.
由
x+a+≤0(0<x<1)恒成立等价于
x+≤-a,
令
μ(x)=x+,则μ(x)在(0,1)上为减函数,所以μ(x)>μ(1)=3,
所以
x+a+≤0(0<x<1)不恒成立.
综上所述a≥-3.
(2)因为
f′(x)=x+a+=
由已知:g(x)=x
2+ax+2b=0的两根为m,n.
则
,即
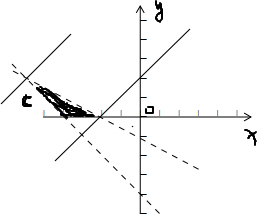
令μ=b-a,则b=a+μ,即μ为过点(a,b)且斜率为1的直线在b轴上的截距,
由
得
,即C(-3,1)
由可行域得:直线过点(-1,0),(-3,1)时,μ分别取最小值1,最大值4.
所以1<b-a<4.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.掌握不等式恒成立时所取的条件.同时考查了简单线性规划的问题.
练习册系列答案
相关题目


