题目内容
6．设地球半径为R，则北纬45°圈上两点A，B的经度分别是西经120°和东经150°，A，B两点的球面距离为$\frac{πR}{3}$．分析 A、B两地在同一纬度圈上，计算经度差，求出AB弦长，以及球心角，然后求出球面距离．
解答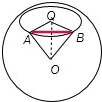 
解：地球表面上从B地（北纬45°，东经150°）到A地（北纬45°，西经120°）
AB的纬圆半径是 $\frac{\sqrt{2}R}{2}$，经度差是90°，
所以AB=R
球心角是 $\frac{π}{3}$，
A、B两地的球面距离是 $\frac{πR}{3}$
故答案为：$\frac{πR}{3}$．
点评 本题考查球面距离及其他计算，考查空间想象能力，是中档题．
练习册系列答案
阅读快车系列答案
相关题目