题目内容
(本题14分)
已知向量 动点
动点 到定直线
到定直线 的距离等于
的距离等于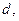 并且满足
并且满足 其中O是坐标原点,
其中O是坐标原点, 是参数.
是参数.
(I)求动点 的轨迹方程,并判断曲线类型;
的轨迹方程,并判断曲线类型;
(Ⅱ) 当 时,求
时,求 的最大值和最小值;
的最大值和最小值;
(Ⅲ) 如果动点M的轨迹是圆锥曲线,其离心率 满足
满足 求实数
求实数 的取值范围.
的取值范围.
解:(1)设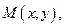 由题设可得
由题设可得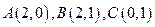
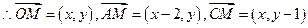
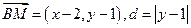 ,
,
因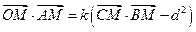
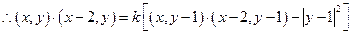
即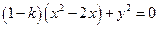 为所求轨迹方程。 …………………………2分
为所求轨迹方程。 …………………………2分
当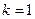 时,
时,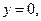 动点
动点 的轨迹是一条直线;
的轨迹是一条直线;
当 时,
时, 动点
动点 的轨迹是圆;
的轨迹是圆;
当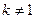 时,方程可化为
时,方程可化为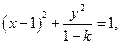 当
当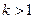 时,动点
时,动点 轨迹是双曲线;
轨迹是双曲线;
当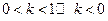 时,动点
时,动点 的轨迹是椭圆。………………………6分
的轨迹是椭圆。………………………6分
(2)当
 时,
时,  的轨迹方
的轨迹方 程为
程为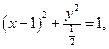
得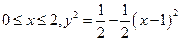
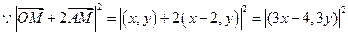
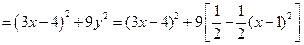

∴当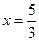 时,
时,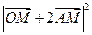 取最小值
取最小值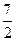
当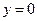 时,
时,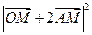 取最大值16.
取最大值16.
因此,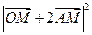 的最小值是
的最小值是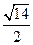 ,最大值是4. …………………10分
,最大值是4. …………………10分
(3)由于 即
即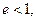 此时圆锥曲线是椭圆,
此时圆锥曲线是椭圆,
其方程可化为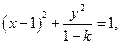
①当 时,
时,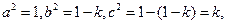
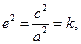
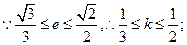 …………………………………………12分
…………………………………………12分
② 当
当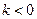 时,
时,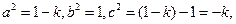
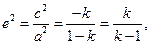
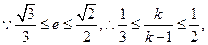 而
而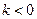 得,
得,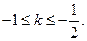
综上, 的取值范围是
的取值范围是 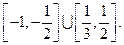 …………………………14分
…………………………14分
解析

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
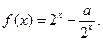 将
将 的图象向右平移2个单位,得到
的图象向右平移2个单位,得到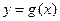 的图象.
的图象.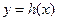 与函数
与函数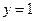 对称,求函数
对称,求函数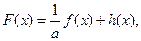 已知
已知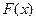 的最小值是
的最小值是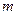 ,且
,且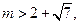 求实数
求实数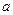 的
的 取值范围.
取值范围.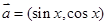 ,
,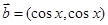 ,
,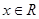 ,函数
,函数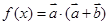
 的最大值与最小正周期;
的最大值与最小正周期; 成立的
成立的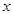 的取值集合.
的取值集合.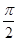 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的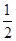 倍得到
倍得到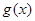 ,关于
,关于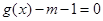 在
在 有且仅有一个解,求
有且仅有一个解,求 的取值范围。
的取值范围。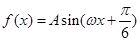 (其中
(其中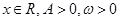 )的图象与
)的图象与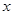 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为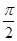 ,且图象上一个点为
,且图象上一个点为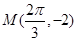 .
.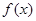 的解析式;
的解析式;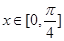 求函数
求函数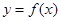 的图象向左平移
的图象向左平移 (a>b>0)的离心率为
(a>b>0)的离心率为 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.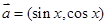 ,
,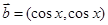 ,
,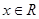 ,函数
,函数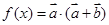
 的最大值与最小正周期;
的最大值与最小正周期;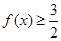 成立的
成立的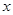 的取值集合.
的取值集合.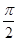 个单位,再把图象所有点的横坐标缩短到原来的
个单位,再把图象所有点的横坐标缩短到原来的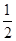 倍得到
倍得到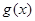 ,关于
,关于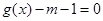 在
在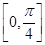 有且仅有一个解,求
有且仅有一个解,求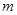 的取值范围。
的取值范围。