题目内容
函数f(x)=Msin(ωx+φ)(ω>0)在区间[a,b]上是增函数,且f(b)=M,f(a)=-M,则函数g(x)=Mcos(ωx+φ)在区间[a,b]上( )
| A.是增函数 |
| B.是减函数 |
| C.可取得最大值M |
| D.可取得最小值-M |
C
试题分析:∵函数f(x)在区间[a,b]上是增函数,且f(a)=-M,f(b)=M
∴M>0且区间[a,b]关于原点对称, 从而函数函数f(x)为奇函数φ=2kπ,
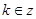 。
。∴函数g(x)=Mcos(ωx+φ)=Mcoswx在区间[a,0]是增函数,[0,b]减函数,
∴函数g(x)=Mcos(ωx+φ)在区间[a,b]上取得最大值M,故选C.
点评:中档题,本题利用整体思想,研究函数的单调性,在解题过程中,熟练运用相关结论:y=Asin(wx+φ)为奇(偶)函数⇒φ=kπ(φ=kπ+
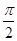 )(k∈Z),是解题的关键。
)(k∈Z),是解题的关键。
练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
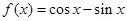 把
把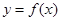 的图象按向量
的图象按向量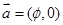 (
(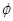 >0)平移后,恰好得到函数
>0)平移后,恰好得到函数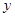 =
=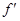 (
(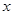 )的图象,则
)的图象,则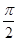
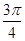
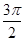
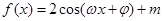 对任意实数
对任意实数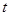 都有
都有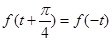 ,且
,且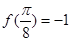 ,则实数
,则实数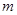 的值等于( )
的值等于( )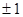
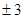
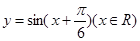 图像上所有的点向左平行移动
图像上所有的点向左平行移动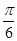 个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图像的解析式为( )
个单位长度,再把图像上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图像的解析式为( )



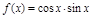 ,给出下列五个说法:
,给出下列五个说法: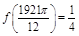 .②若
.②若 ,则
,则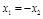 .③
.③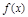 在区间
在区间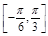 上单调递增. ④将函数
上单调递增. ④将函数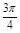 个单位可得到
个单位可得到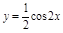 的图象.⑤
的图象.⑤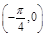 成中心对称.其中正确说法的序号是 .
成中心对称.其中正确说法的序号是 .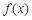 既是奇函数又是周期函数,若
既是奇函数又是周期函数,若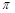 ,且当
,且当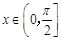 时,
时, 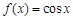 ,则
,则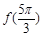 的值为 ( )
的值为 ( )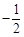
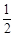
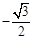
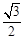
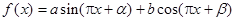 ,其中
,其中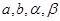 为非零常数. 若
为非零常数. 若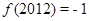 ,则
,则 .
. 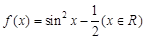 ,则
,则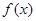 是
是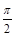 的奇函数
的奇函数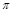 的奇函数
的奇函数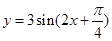 的最小正周期为
的最小正周期为