题目内容
过双曲线
-
=1(a>0,b>0)的右焦点F作圆x2+y2=a2的切线FM,交y轴于点P,切圆于点M,若2
=
+
,则双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| OM |
| OF |
| OP |
A、
| ||
B、
| ||
| C、2 | ||
D、
|
分析:根据向量加法法则,得到OM是△POF中PF边上的中线.由PF与圆x2+y2=a2相切得到OM⊥PF,从而可得△POF是等腰直角三角形,∠MF0=45°.最后在Rt△OMF利用三角函数的定义算出
=
,可得双曲线的离心率大小.
| a |
| c |
| ||
| 2 |
解答:解: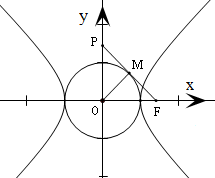 ∵2
∵2
=
+
,
∴△POF中,OM是PF边上的中线.
∵PF与圆x2+y2=a2相切,∴OM⊥PF,
由此可得△POF中,PO=FO,∠MF0=45°,
又∵Rt△OMF中,OM=a,OF=c,
∴sin∠MF0=
=
,即
=
.
因此,双曲线的离心率e=
=
.
故选:D
 ∵2
∵2| OM |
| OF |
| OP |
∴△POF中,OM是PF边上的中线.
∵PF与圆x2+y2=a2相切,∴OM⊥PF,
由此可得△POF中,PO=FO,∠MF0=45°,
又∵Rt△OMF中,OM=a,OF=c,
∴sin∠MF0=
| OM |
| OF |
| ||
| 2 |
| a |
| c |
| ||
| 2 |
因此,双曲线的离心率e=
| c |
| a |
| 2 |
故选:D
点评:本题在双曲线中给出向量关系式,在直线与圆相切的情况下求双曲线的离心率.着重考查了解直角三角形、向量的加法法则、直线与圆的位置关系和双曲线的简单性质等知识,属于中档题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
过双曲线
-
=1的左焦点F作⊙O:x2+y2=a2的两条切线,记切点为A,B,双曲线左顶点为C,若∠ACB=120°,则双曲线的渐近线方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、y=±
| ||||
B、y=±
| ||||
C、y=±
| ||||
D、y=±
|