题目内容
【题目】如图,四棱锥 ![]() 中,底面ABCD是直角梯形,
中,底面ABCD是直角梯形, ![]() ,
, ![]() ,平面
,平面 ![]() 底面ABCD, O为AD的中点, M是棱PC上的点, AD=2AB.
底面ABCD, O为AD的中点, M是棱PC上的点, AD=2AB.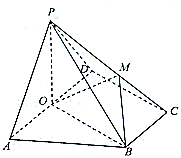
(1)求证:平面 ![]() 平面PAD;
平面PAD;
(2)若 ![]() 平面BMO,求
平面BMO,求 ![]() 的值.
的值.
【答案】
(1)解:证明:∵ ![]() ,
, ![]() , O为AD的中点,
, O为AD的中点,
∴四边形BCDO为平行四边形,∴ ![]() .
.
∵ ![]() ,∴
,∴ ![]() ,即
,即 ![]() .
.
又∵平面 ![]() 平面ABCD ,且平面
平面ABCD ,且平面 ![]() 平面
平面 ![]() ,
,
∴ ![]() 平面PAD.∵
平面PAD.∵ ![]() 平面POB,∴平面
平面POB,∴平面 ![]() 平面PAD
平面PAD
(2)解:连接AC,交BO于N,连结MN,
∵ ![]() 平面BMO,平面
平面BMO,平面 ![]() 平面PAC=MN,∴
平面PAC=MN,∴ ![]() ,
,
又∵ ![]() , O为AD中点,AD=2AB,
, O为AD中点,AD=2AB,
∴N是AC的中点,
∴M是PC的中点,则 ![]()
【解析】(1)由已知可得CD ⊥ A D,利用题中的已知条件可证出O B ⊥ A D,根据线面垂直的判定定理可证出B O ⊥ 平面PAD,再由面面垂直的判定定理可得证面面垂直。(2)根据题意作出辅助线,由线面平行的性质定理即可证明P A / / M N,再结合中位线的性质转化已知条件即可求出比值。

练习册系列答案
相关题目