题目内容
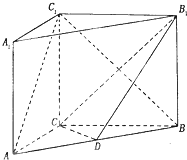 如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.(1)求证:AC1∥平面CDB1.
(2)求证:AC⊥BC1;
(3)求直线B1D与平面CBB1C1所成角的正玄值.
分析:(1)利用线面平行的判定定理即可证明;
(2)利用线面垂直的性质定理即可证明;
(3)先作出线面角,进而求出即可.
(2)利用线面垂直的性质定理即可证明;
(3)先作出线面角,进而求出即可.
解答:证明:(1)连接BC1、CB1,相较于点O,则BO=OC1.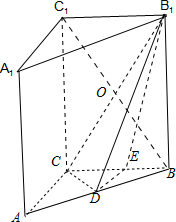
又∵点D是AB的中点.∴OD∥AC1.
∵OD?平面CDB1,AC1?平面CDB1.
∴AC1∥平面CDB1.
(2)∵AC=3,AB=5,BC=4,
∴AB2=AC2+CB2,
∴∠ACB=90°,∴AC⊥CB;
∵直三棱柱ABC-A1B1C1,∴CC1⊥AC,
又∵CC1∩CB=C,
∴AC⊥平面CBB1C1,
∴AC⊥BC1.
(3)取CB的中点E,连接DE、EB1.
则DE∥AC,DE=
AC=
.
∵AC⊥平面CBB1C1,
∴DE⊥平面CBB1C1,
∴∠DB1E是直线DB1与平面CBB1C1所成的角.
在Rt△BB1E中,B1E=
=2
.
∴DB1=
=
.
∴sin∠DB1E=
=
.

又∵点D是AB的中点.∴OD∥AC1.
∵OD?平面CDB1,AC1?平面CDB1.
∴AC1∥平面CDB1.
(2)∵AC=3,AB=5,BC=4,
∴AB2=AC2+CB2,
∴∠ACB=90°,∴AC⊥CB;
∵直三棱柱ABC-A1B1C1,∴CC1⊥AC,
又∵CC1∩CB=C,
∴AC⊥平面CBB1C1,
∴AC⊥BC1.
(3)取CB的中点E,连接DE、EB1.
则DE∥AC,DE=
| 1 |
| 2 |
| 3 |
| 2 |
∵AC⊥平面CBB1C1,
∴DE⊥平面CBB1C1,
∴∠DB1E是直线DB1与平面CBB1C1所成的角.
在Rt△BB1E中,B1E=
| 22+42 |
| 5 |
∴DB1=
(
|
| ||
| 2 |
∴sin∠DB1E=
| DE |
| DB1 |
3
| ||
| 89 |
点评:熟练掌握线面平行、垂直的判定定理与性质定理和线面角的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目




