题目内容
(本小题满分13分)
专家通过研究学生的学习行为,发现学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增,中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设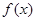 表示学生注意力随时间
表示学生注意力随时间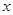 (分钟)的变化规律(
(分钟)的变化规律(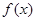 越大,表明学生注意力越大),经过试验分析得知:
越大,表明学生注意力越大),经过试验分析得知: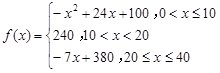
(Ⅰ)讲课开始后多少分钟,学生的注意力最集中?能坚持多少分钟?
(Ⅱ)讲课开始后5分钟时与讲课开始后25分钟时比较,何时学生的注意力更集中?
(Ⅲ)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲完这道题目?
(1) 坚持10分钟(2) 学生的注意力比讲课开始后5分钟时更集中(3) 经过适当安排,老师能在学生达到所需的状态下讲完这道题目
解析试题分析:解:(Ⅰ)当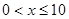 时,
时, 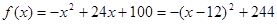 是增函数,
是增函数,
且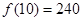
当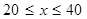 时,
时, 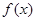 是减函数,且
是减函数,且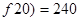
所以讲课开始10分钟,学生的注意力最集中,能坚持10分钟. ………………………5分
(Ⅱ)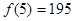 ,
,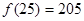 ,所以讲课开始后25分钟时,学生的注意力比讲课开始后5分钟时更集中. ……………8分
,所以讲课开始后25分钟时,学生的注意力比讲课开始后5分钟时更集中. ……………8分
(Ⅲ) 当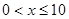 时,令
时,令 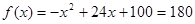 得
得 .
.
当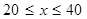 时令
时令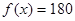 ,得
,得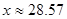
所以学生的注意力在180以上,所持续的时间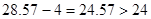
所以经过适当安排,老师能在学生达到所需的状态下讲完这道题目. …………………13分
考点:本试题考查了函数模型的运用。
点评:构造二次函数模型,函数解析式求解是关键,解决实际问题通常有四个步骤:(1)阅读理解,认真审题;(2)引进数学符号,建立数学模型;(3)利用数学的方法,得到数学结果;(4)转译成具体问题作出解答,其中关键是建立数学模型.

练习册系列答案
相关题目
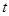 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于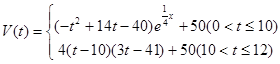
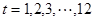 ),问:同一年内哪些月份是枯水期?
),问:同一年内哪些月份是枯水期?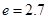 计算)
计算)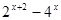
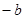 =0.
=0.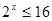 且
且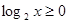 ,求实数b的取值范围.
,求实数b的取值范围.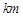 的A,B两家工厂(视作污染源)的污染强度分别为
的A,B两家工厂(视作污染源)的污染强度分别为 ,它们连线上任意一点C处的污染指数
,它们连线上任意一点C处的污染指数 等于两家工厂对该处的污染指数之和.设
等于两家工厂对该处的污染指数之和.设 (
(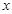 的函数;
的函数;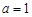 ,且
,且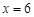 时,
时, 的值.
的值. 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽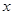 及长
及长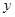 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.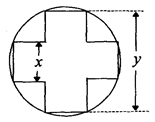
 (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点. ·
·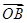 的值;
的值; 、
、 的终边上,求tan(
的终边上,求tan(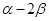 )的值.
)的值.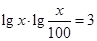 .
.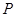 (元)之间的关系为
(元)之间的关系为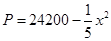 ,且生产
,且生产 吨的成本为
吨的成本为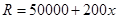 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)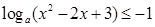 ,当
,当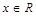 时恒成立.求
时恒成立.求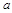 的取值范围.
的取值范围.