题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且椭圆上的点到焦点的最长距离为
,且椭圆上的点到焦点的最长距离为![]() .
.
(1)求椭圆C的方程;
(2)过点P(0,2)的直线l(不过原点O)与椭圆C交于两点A、B,M为线段AB的中点.
(ⅰ)证明:直线OM与l的斜率乘积为定值;
(ⅱ)求△OAB面积的最大值及此时l的斜率.
【答案】(1)![]() ;(2)(ⅰ)详见解析;(ⅱ)△AOB面积的最大值是
;(2)(ⅰ)详见解析;(ⅱ)△AOB面积的最大值是![]() ,此时l的斜率为±
,此时l的斜率为±![]() .
.
【解析】
(1)由题意得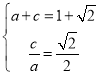 ,解得即可求出方程,
,解得即可求出方程,
(2)(i)设直线l为:y=kx+2,根据韦达定理和斜率公式即可求出,
(ii)先根据弦长公式求出|AB|及原点到直线的距离,再令![]() =t,表示出三角形的面积,利用基本不等式即可求出.
=t,表示出三角形的面积,利用基本不等式即可求出.
解:(1)由题意得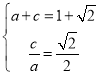 ,解得
,解得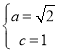 ,
,
∴a2=2,b2=a2-c2=1,
∴椭圆C的方程为![]() ;
;
(2)(ⅰ)设直线l为:y=kx+2,A(x1,y1),B(x2,y2),M(xM,yM),
由题意得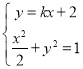 ,∴(1+2k2)x2+8kx+6=0,
,∴(1+2k2)x2+8kx+6=0,
∴△=8(2k2-3)>0,即![]() ,
,
由韦达定理得:x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴直线OM与l的斜率乘积为定值.
(ⅱ)由(ⅰ)可知: 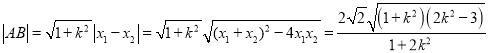 ,
,
原点到直线AB的距离为![]()
令![]() =t,则t>0,
=t,则t>0,
∴S△AOB=![]() =
=![]() ≤
≤![]() =
=![]() ,
,
当且仅当t=2时等号成立,此时k=±![]() ,且满足△>0,
,且满足△>0,
∴△AOB面积的最大值是![]() ,此时l的斜率为±
,此时l的斜率为±![]() .
.

【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有95%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,求所抽取的5人中“微信控”和“非微信控”的人数;
(3)从(2)中抽取的5位女性中,再随机抽取3人赠送礼品,试求抽取3人中恰有2人位“微信控”的概率.
参考公式: 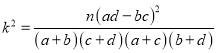 ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |