题目内容
已知椭圆M:| x2 |
| a2 |
| y2 |
| b2 |
|
| π |
| 4 |
(Ⅰ)试求椭圆M的方程;
(Ⅱ)若斜率为
| 1 |
| 2 |
| 3 |
| 2 |
分析: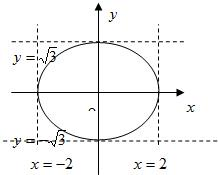 (Ⅰ)平面区域Ω:
(Ⅰ)平面区域Ω:
是一个矩形区域,如图所示.
依题意及几何概型,可得
=
,由此可导出椭圆M的方程.
(Ⅱ)设直线l的方程为:y=
x+b,C(x1,y1),D(x2,y2)
联立直线l'的方程与椭圆方程得:
,
∴3x2+4(
x+b)2=12,
然后结合题设条件,由根的判别式和根与系数的关系能够推导出k1+k2为定值0.
 (Ⅰ)平面区域Ω:
(Ⅰ)平面区域Ω:
|
依题意及几何概型,可得
| πab | ||
8
|
| π |
| 4 |
(Ⅱ)设直线l的方程为:y=
| 1 |
| 2 |
联立直线l'的方程与椭圆方程得:
|
∴3x2+4(
| 1 |
| 2 |
然后结合题设条件,由根的判别式和根与系数的关系能够推导出k1+k2为定值0.
解答: 解:(Ⅰ)平面区域Ω:
解:(Ⅰ)平面区域Ω:
是一个矩形区域,如图所示.
依题意及几何概型,可得
=
,
即ab=2
.
因为0<a≤2,0<b≤
,
所以,a=2,b=
.
所以,椭圆M的方程为
+
=1
(Ⅱ)设直线l的方程为:y=
x+b,C(x1,y1),D(x2,y2)
联立直线l'的方程与椭圆方程得:
(1)代入(2)得:3x2+4(
x+b)2=12
化简得:x2+bx+b2-3=0)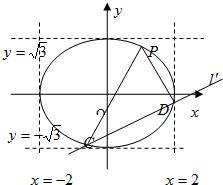
当△>0时,即,b2-4(b2-3)>0
也即,|b|<2时,直线l'与椭圆有两交点,
由韦达定理得:
,
所以,k1=
=
,
k2=
=
则k1+k2=
+
=
=
=0
所以,k1+k2为定值.
 解:(Ⅰ)平面区域Ω:
解:(Ⅰ)平面区域Ω:
|
依题意及几何概型,可得
| πab | ||
8
|
| π |
| 4 |
即ab=2
| 3 |
因为0<a≤2,0<b≤
| 3 |
所以,a=2,b=
| 3 |
所以,椭圆M的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)设直线l的方程为:y=
| 1 |
| 2 |
联立直线l'的方程与椭圆方程得:
|
(1)代入(2)得:3x2+4(
| 1 |
| 2 |
化简得:x2+bx+b2-3=0)

当△>0时,即,b2-4(b2-3)>0
也即,|b|<2时,直线l'与椭圆有两交点,
由韦达定理得:
|
所以,k1=
y1-
| ||
| x1-1 |
| ||||
| x1-1 |
k2=
y2-
| ||
| x2-1 |
| ||||
| x2-1 |
则k1+k2=
| ||||
| x1-1 |
| ||||
| x2-1 |
| x1•x2+(b-2)(x1+x2)+3-2b |
| (x1-1)(x2-1) |
| b2-3+(b-2)(-b)+3-2b |
| (x1-1)(x2-1) |
所以,k1+k2为定值.
点评:本题综合考查椭圆的性质及应用和直线 与椭圆的位置关系,解题时要认真审题、仔细解答,避免出现不必要的错误.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目