Question

已知双曲线C的中心在原点，抛物线的焦点是双曲线C

的一个焦点，且双曲线过点（1, ）.     (1)求双曲线的方程;

（2）设直线:与双曲线C交于A、B两点, 试问:

① 为何值时

② 是否存在实数, 使A、B两点关于直线对称(为常数), 若存在, 求出的值; 若不存在,

Answer 1

解: (1) 由题意设双曲线方程为,把(1,)代入得（*）

又的焦点是（，0），故双曲线的与（*）

联立，消去可得，.

∴ ，（不合题意舍去）

于是，∴ 双曲线方程为

 (2) 由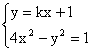消去得（*），当

 即（）时，与C有两个交点A、B     

① 设A（，），B（，），因，故

即，由（*）知，，代入可得

 化简得∴ ，检验符合条件，故当时，

② 若存在实数满足条件，则必须

 由（2）、（3）得………（4）

把代入（4）得                     

这与（1）的矛盾，故不存在实数满足条件.