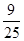题目内容
设
，则函数
在区间[1，2]上有零点的概率是（ ）
，则函数在区间[1，2]上有零点的概率是（ ）A． | B． |
C． | D． |
C
解：由f（x）在实数集上单调递增可知，要使函数f（x）=x3+ax-b在区间[1，2]上有零点，只需满足条件 f(1)≤0 f(2)≥0 ，
从而解得b-a≥1且b-2a≤8，∴a+1≤b≤2a+8，
∴当a=1时，b取2，4，8；
a=2时b取4，8，12；
a=3时，b取4，8，12；a=4时b取8，12；
共11种取法，
又∵a，b的总共取法有16种，
故答案为：11 /16 ，
故选C．
从而解得b-a≥1且b-2a≤8，∴a+1≤b≤2a+8，
∴当a=1时，b取2，4，8；
a=2时b取4，8，12；
a=3时，b取4，8，12；a=4时b取8，12；
共11种取法，
又∵a，b的总共取法有16种，
故答案为：11 /16 ，
故选C．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
，乙队中3人答对的概率分别为
，且各人回答正确与否相互之间没有影响.用
表示甲队的总得分. 
的概率及
； 
.
个面的中心，甲从这
