题目内容
3.已知${(2x+\root{3}{x^2})^n}$的展开式中,倒数第3项的二项式系数为45,(1)求展开式中x5的项;
(2)求二项式系数最大的项.
分析 (1)由倒数第3项的二项式系数为45列式求得n值,然后写出二项展开式的通项,由x的指数等于5求得r值,则答案可求;
(2)由(1)可得展开式共有11项,得到第6项的二项式系数最大,由此求得最大项.
解答 解:(1)由${C}_{n}^{2}=45$,得n=10,
${T}_{r+1}={C}_{10}^{r}(2x)^{10-r}({x}^{\frac{2}{3}})^{r}={C}_{10}^{r}{2}^{10-r}{x}^{10-\frac{5}{3}r}$,
令10-$\frac{5}{3}r=5$,得r=3.
∴${T}_{4}={C}_{10}^{3}{2}^{7}{x}^{5}=15360{x}^{5}$;
(2)由(1)知,展开式共有11项,
∴第6项的二项式系数最大,${T}_{6}=8024{x}^{\frac{25}{3}}$.
点评 本题考查二项式系数的性质,关键是熟记二项展开式的通项及应用,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.若△ABC中,a=2bcosC,且sin2B+sin2C=2sin2A,则该三角形一定为( )
| A. | 等腰直角三角形 | B. | 等腰钝角三角形 | ||
| C. | 等边三角形 | D. | 不存在这样的三角形 |
18.定义在R上的函数f(x)满足:f′(x)>1-f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或x>1} | D. | {x|x<-1或0<x<1} |
8.下列函数中,既是偶函数,又在区间(0,+∞)单调递减的是( )
| A. | y=cosx | B. | y=lg|x| | C. | y=-x2+1 | D. | y=x3 |
13.复数$\frac{1+2i}{1+i}$的共轭复数等于( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{3}{2}$+$\frac{1}{2}$i | D. | $\frac{3}{2}$-$\frac{1}{2}$i |

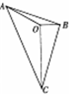 如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.
如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.