题目内容
【题目】[选修4-4:坐标系与参数方程]
已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1,  (t为参数).
(t为参数).
(1)求曲线C1上的点到曲线C2距离的最小值;
(2)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的 ![]() 倍,得到曲线
倍,得到曲线 ![]() .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 ![]() 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|.
【答案】
(1)解:∵曲线C1:ρ=1,∴曲线C1的直角坐标方程为:x2+y2=1,
∴圆心为(0,0),半径为r=1,
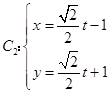 (t为参数)消去参数t的C2:y=x+2,
(t为参数)消去参数t的C2:y=x+2,
∴圆心到直线距离d= ![]() ,
,
∴曲线C1上的点到曲线C2距离的最小值为 ![]() .
.
(2)解:∵把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的 ![]() 倍,得到曲线
倍,得到曲线 ![]() .
.
∴伸缩变换为 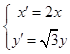 ,∴曲线
,∴曲线 ![]() :
: ![]() =1,
=1,
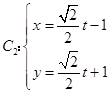 (t为参数)代入曲线
(t为参数)代入曲线 ![]() ,整理得
,整理得 ![]() .
.
∵t1t2<0,
∴|PA|+|PB|=|t1|+|t2|=|t1﹣t2|= ![]() .
.
【解析】(1)求出曲线C1的直角坐标方程为:x2+y2=1,C2:y=x+2,再求出圆心到直线距离,由此能求出曲线C1上的点到曲线C2距离的最小值.(2)伸缩变换为 ![]() ,从而曲线
,从而曲线 ![]() :
: ![]() =1,
=1,  (t为参数)代入曲线
(t为参数)代入曲线 ![]() ,得
,得 ![]() .由此能求出|PA|+|PB|.
.由此能求出|PA|+|PB|.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如表:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(Ⅰ)试分别估计芯片甲,芯片乙为合格品的概率;
(Ⅱ)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.