题目内容
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)试运用独立性检验的思想方法点拨:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由.(参考下表)

解:(1)积极参加班级工作的学生有24人,总人数为50人,概率为 ;
;
不太主动参加班级工作且学习积极性一般的学生有19人,概率为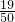 .
.
(2) ,
,
∵K2>6.635,
∴有99%的把握说学习积极性与对待班级工作的态度有关系.
分析:(1)是一古典概型问题,把基本事件的总数与满足要求的个数找出来,代入古典概率的计算公式即可.
(2)是独立性检验的应用,由题中的数据,计算出k2与临界值比较即可得出结论
点评:本题把独立性检验,概率的求法,列联表等知识联系在一起,是道综合性题,难度不大,符合新课标对于本部分的要求,希望通过本题把相关知识掌握好.
 ;
;不太主动参加班级工作且学习积极性一般的学生有19人,概率为
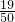 .
.(2)
 ,
,∵K2>6.635,
∴有99%的把握说学习积极性与对待班级工作的态度有关系.
分析:(1)是一古典概型问题,把基本事件的总数与满足要求的个数找出来,代入古典概率的计算公式即可.
(2)是独立性检验的应用,由题中的数据,计算出k2与临界值比较即可得出结论
点评:本题把独立性检验,概率的求法,列联表等知识联系在一起,是道综合性题,难度不大,符合新课标对于本部分的要求,希望通过本题把相关知识掌握好.

练习册系列答案
相关题目
某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,其中学习积极性高的同学中,积极参加班级工作的有18名,不太主动参加班级工作的有7名;学习积极性一般的同学中,积极参加班级工作的有6名,不太主动参加班级工作的有19名.
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?
参考公式:K2统计量的表达式是:K2=
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?
参考公式:K2统计量的表达式是:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
根据表中数据得到K2=
≈5.059,因为p(K2≥5.024)=0.025,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
| 认为作业多 | 认为作业不多 | 总数 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
| 50×(18×15-8×9)2 |
| 27×23×24×26 |
| A、97.5% | B、95% |
| C、90% | D、无充分根据 |
某班主任对全班50名学生进行迟到与学习成绩是否有关的调查,数据如下表:
|
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
根据表中数据,则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为 .
| 认为作业多 | 认为作业不多 | 总数 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |