题目内容
在△ABC中,O为中线AM上的一个动点,若 ,则
,则 的最小值是
的最小值是
【答案】
-2
【解析】
试题分析:
由题意画出草图分析,由于在△ABC中,O为中线AM上的一个动点,所以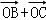 =2
=2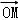 ,所以
,所以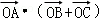 ═
═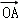 ?2
?2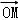 ,而|OA|+|OM|=2≥2
,而|OA|+|OM|=2≥2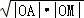 利用均值不等式即可求得解:由题意画出草图:
利用均值不等式即可求得解:由题意画出草图:
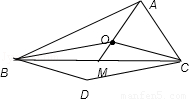
由于点M为△ABC中边BC的中点,∴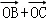 =2
=2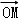 ,
,
∴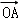 ?(
?(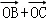 )=
)=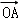 ?2
?2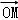 =﹣2|OA|?|OM|.
=﹣2|OA|?|OM|.
∵O为中线AM上的一个动点,即A、O、M三点共线
∴|AM|=|OA|+|OM|=2≥2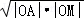 (当且仅当“OA=OM“时取等号)?|OA|?|OM|≤1,
(当且仅当“OA=OM“时取等号)?|OA|?|OM|≤1,
又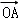 ?2
?2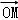 =﹣2|OA|?|OM|≥﹣2,所以则
=﹣2|OA|?|OM|≥﹣2,所以则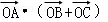 的最小值为﹣2.
的最小值为﹣2.
故答案为-2.
考点:三角形的中线
点评:该试题考查了三角形的中线以及向量的平行四边形法则的运用,属于基础题。

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
在△ABC中,O为外心,P是平面内点,且满足
+
+
=
,则P是△ABC的( )
| OA |
| OB |
| OC |
| OP |
| A、外心 | B、内心 | C、重心 | D、垂心 |