题目内容
在△ABC中，O为平面上一定点，动点P满足
=
+λ(
+
)，λ∈[0，+∞），则P的轨迹一定通过△ABC的（ ）
| OP |
| OA |
| AB |
| AC |
分析：设BC的中点为D，则AD为△ABC中BC边上的中线，利用向量的线性运算，可得P、A、D三点共线，从而可得结论．
解答：解：设BC的中点为D，则AD为△ABC中BC边上的中线
∴
=
+λ(
+
)=
+2λ
∴
=2λ
∴P、A、D三点共线
∴P的轨迹一定通过△ABC的重心
故选C．
∴
| OP |
| OA |
| AB |
| AC |
| OA |
| AD |
∴
| AP |
| AD |
∴P、A、D三点共线
∴P的轨迹一定通过△ABC的重心
故选C．
点评：本题主要考查平面向量的基本定理和向量的共线定理．属中档题．
练习册系列答案
通城学典默写能手系列答案
相关题目
＝
＋
＋
，且
·
＝8，则边AC上的高h的最大值为________．
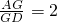；空间中：在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则
=________．
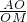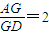；空间中：在正四面体ABCD中，若三角形BCD中心为M，正四面体ABCD中心为O，则
= ．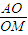