题目内容
(本小题满分10分)选修4-1:几何证明选讲
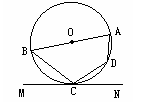
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证: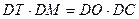 ;
;
(2)若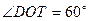 ,试求
,试求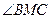 的大小.
的大小.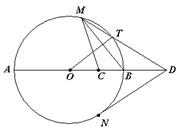
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M、T(不与A、B重合),DN与圆O相切于点N,连结MC,MB,OT.
(1)求证:
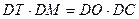 ;
;(2)若
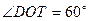 ,试求
,试求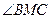 的大小.
的大小.
(1)证明见解析
(2)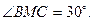
(2)
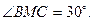
(1)证明:因MD与圆O相交于点T,由切割线定
理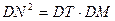 ,
,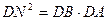 ,得
,得
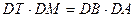 ,设半径OB=
,设半径OB=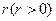 ,
,
因BD=OB,且BC=OC=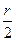 ,
,
则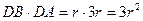 ,
,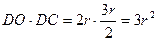 ,
,
所以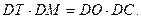
(2)由(1)可知,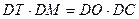 ,
,
且 ,
,
故 ∽
∽ ,所以
,所以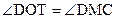 ;
;
根据圆周角定理得,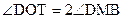 ,则
,则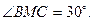
理
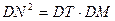 ,
,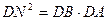 ,得
,得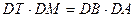 ,设半径OB=
,设半径OB=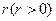 ,
,因BD=OB,且BC=OC=
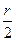 ,
,则
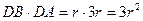 ,
,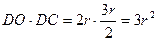 ,
,所以
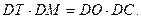
(2)由(1)可知,
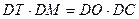 ,
,且
 ,
,故
 ∽
∽ ,所以
,所以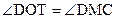 ;
;根据圆周角定理得,
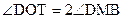 ,则
,则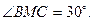

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 小题满分10分)如图5,⊙O1和⊙O2公切线AD和BC相交于点D,A、B、C为切点,直线DO1与⊙O1与E、G两点,直线DO2交⊙O2与F、H两点。
小题满分10分)如图5,⊙O1和⊙O2公切线AD和BC相交于点D,A、B、C为切点,直线DO1与⊙O1与E、G两点,直线DO2交⊙O2与F、H两点。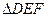 ~
~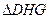 ;
;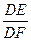 的值。
的值。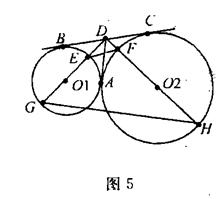
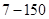 ,四边形
,四边形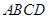 为圆内接四边形,
为圆内接四边形,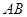 是直径,
是直径,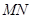 切
切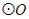 于
于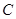 点,
点,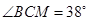 ,那么
,那么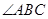 的度数是 ( )
的度数是 ( )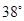
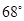
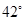

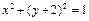
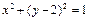
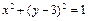
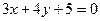 相切的圆的标准方程是
相切的圆的标准方程是 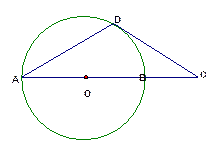
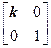 ,N=
,N=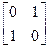 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值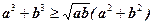
 为⊙O的直径,弦
为⊙O的直径,弦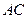 、
、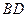 交于点
交于点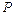 ,若
,若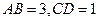 ,则
,则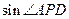 =
= 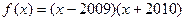 的图像与
的图像与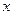 轴、
轴、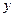 轴有三个不同的交点,有一个圆恰好经过这三个点,则此圆与坐标轴的另一个交点是 ( )
轴有三个不同的交点,有一个圆恰好经过这三个点,则此圆与坐标轴的另一个交点是 ( )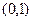
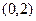
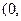
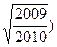
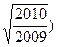
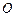 外一点
外一点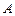 引圆的切线
引圆的切线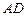 和割线
和割线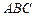 ,已知
,已知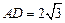 ,
,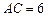 ,圆
,圆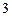 ,则圆心
,则圆心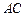 的距离为 .
的距离为 .