题目内容
【题目】设有下列四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :“
:“![]() ”是“
”是“![]() 为奇函数”的充要条件;
为奇函数”的充要条件;
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件.
是递减数列”的充要条件.
其中,真命题的是![]()
![]()
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
【答案】C
【解析】
根据不等式的性质,结合函数奇偶性的性质,等比数列的性质以及充分条件和必要条件的定义分别进行点评即可.
![]() :当
:当![]() ,
,![]() 时,满足
时,满足![]() ,则
,则![]() ;不成立,即命题
;不成立,即命题![]() 是假命题
是假命题
![]() :设
:设![]() ,则
,则![]() ,即
,即![]() 是减函数,
是减函数,
若![]() ,
,![]() ,即
,即![]() ,则
,则![]() 成立,即命题
成立,即命题![]() 是真命题;
是真命题;
若![]() ,则
,则![]() ,即
,即![]() ,函数
,函数![]() 是奇函数,
是奇函数,
当![]() ,满足
,满足![]() 是奇函数,但
是奇函数,但![]() 不成立,即“
不成立,即“![]() ”是“
”是“![]() 为奇函数”的充要条件错误;即命题
为奇函数”的充要条件错误;即命题![]() 是假命题,
是假命题,
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”,则
”,则![]() ,若
,若![]() ,则
,则![]() ,
,
得![]() ,此时
,此时![]() ,即
,即![]() ,数列为递减数列,
,数列为递减数列,
![]() ,则
,则![]() ,
,
则![]() ,此时
,此时![]() ,即
,即![]() ,数列为递减数列,综上等比数列
,数列为递减数列,综上等比数列![]() 是递减数列,
是递减数列,
若等比数列![]() 是递减数列,则
是递减数列,则![]() 成立,
成立,
即等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件,故命题
是递减数列”的充要条件,故命题![]() 是真命题;
是真命题;
故真命题是![]() ,
,![]() ,
,
故选:C.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
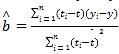 ,
,![]()
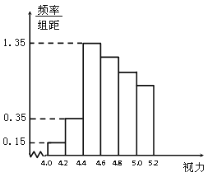
【题目】某学校研究性学习小组对该校高三学生的视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如下直方图:
年级名次/是否近视 | 1-50 | 951-1000 |
近视 | 41 | 32 |
不近视 | 9 | 18 |
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到如上述表格中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系;
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
附:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】改革开放以来,伴随着我国经济持续增长,户均家庭教育投入![]() 户均家庭教育投入是指一个家庭对家庭成员教育投入的总和
户均家庭教育投入是指一个家庭对家庭成员教育投入的总和![]() 也在不断提高
也在不断提高![]() 我国某地区2012年至2018年户均家庭教育投入
我国某地区2012年至2018年户均家庭教育投入![]() 单位:千元
单位:千元![]() 的数据如表:
的数据如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
户均家庭教育投入y |
|
|
|
|
|
|
|
![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() 利用
利用![]() 中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
中的回归方程,分析2012年至2018年该地区户均家庭教育投入的变化情况,并预测2019年该地区户均家庭教育投入是多少.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: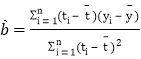 ,
,![]() .
.
