题目内容
已知a,b,c分别是双曲线的实半轴、虚半轴和半焦距,若方程ax2+bx+c=0无实数根,则此双曲线的离心率e的取值范围是 .
【答案】分析:由方程ax2+bx+c=0无实数根可知b2-4ac<0,再根据双曲线的性质推导此双曲线的离心率e的取值范围.
解答:解:由题意可知b2-4ac<0,
∵b2=c2-a2,∴c2-a2-4ac<0,
∴e2-4e-1<0,
解得 .
.
∵e>1,∴ .
.
故双曲线的离心率e的取值范围是 (1,2+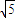 ).
).
答案:(1,2+ ).
).
点评:本题主要考查双曲线的简单性质,解题时要注意双曲线的离心率大于1.
解答:解:由题意可知b2-4ac<0,
∵b2=c2-a2,∴c2-a2-4ac<0,
∴e2-4e-1<0,
解得
 .
.∵e>1,∴
 .
.故双曲线的离心率e的取值范围是 (1,2+
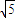 ).
).答案:(1,2+
 ).
).点评:本题主要考查双曲线的简单性质,解题时要注意双曲线的离心率大于1.

练习册系列答案
相关题目