题目内容
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+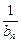 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与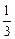 logabn+1的大小,并证明你的结论
logabn+1的大小,并证明你的结论
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga(1+
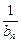 )(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1)记Sn是数列{an}的前n项和,试比较Sn与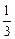 logabn+1的大小,并证明你的结论
logabn+1的大小,并证明你的结论(1)bn=3n-2(2)当a>1时,Sn>
 logabn+1?,当 0<a<1时,Sn<
logabn+1?,当 0<a<1时,Sn< logabn+1
logabn+1设数列{bn}的公差为d,由题意得
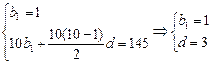 ,∴bn=3n-2
,∴bn=3n-2(2)证明:由bn=3n-2知
Sn=loga(1+1)+loga(1+
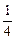 )+…+loga(1+
)+…+loga(1+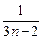 )
)=loga[(1+1)(1+
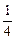 )…(1+
)…(1+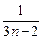 )]
)]而
 logabn+1=loga
logabn+1=loga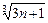 ,于是,比较Sn与
,于是,比较Sn与 logabn+1?的大小
logabn+1?的大小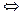 比较(1+1)(1+
比较(1+1)(1+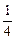 )…
)…(1+
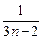 )与
)与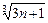 的大小.
的大小.取n=1,有(1+1)=
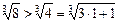
取n=2,有(1+1)(1+
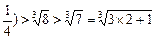
推测:(1+1)(1+
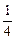 )…(1+
)…(1+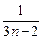 )>
)>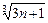 (*)
(*)①当n=1时,已验证(*)式成立.
②假设n=k(k≥1)时(*)式成立,即(1+1)(1+
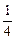 )…(1+
)…(1+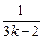 )>
)>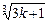
则当n=k+1时,
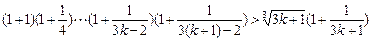
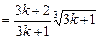
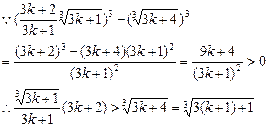
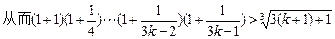 ,即当n=k+1时,(*)式成立
,即当n=k+1时,(*)式成立由①②知,(*)式对任意正整数n都成立.
于是,当a>1时,Sn>
 logabn+1?,当 0<a<1时,Sn<
logabn+1?,当 0<a<1时,Sn< logabn+1
logabn+1
练习册系列答案
相关题目
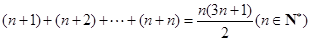
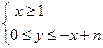 表示的平面区域内可行解的个数,则f(1)=_______;f(2)=_______;f(n)=_______.
表示的平面区域内可行解的个数,则f(1)=_______;f(2)=_______;f(n)=_______.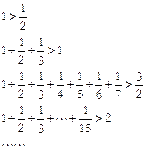
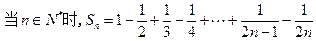
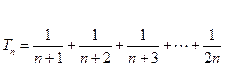
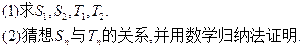
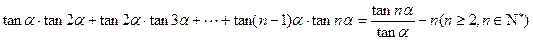
 .
.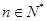 时,
时, 成立
成立 的过程中,当n=k到n=k+1时,左边所增加的项为________________
的过程中,当n=k到n=k+1时,左边所增加的项为________________