题目内容
【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,anan+1=2Sn , 设bn= ![]() ,若存在正整数p,q(p<q),使得b1 , bp , bq成等差数列,则p+q= .
,若存在正整数p,q(p<q),使得b1 , bp , bq成等差数列,则p+q= .
【答案】5
【解析】解:数列{an}满足a1=1,anan+1=2Sn , ∴n=1时,a1a2=2S1=2a1 , 解得a2=2.n≥2时,2an=2(Sn﹣Sn﹣1)=an(an+1﹣an﹣1),∵an≠0,∴an+1﹣an﹣1=2. ∴数列{an}是首项为1,公差为1的等差数列,∴an=1+n﹣1=n.
∴bn= ![]() =
= ![]() .
.
∵存在正整数p,q(p<q),使得b1 , bp , bq成等差数列,
∴2bp=b1+bq , ∴ ![]() =
= ![]() (*).
(*).
∵数列{bn}是单调递减数列.
当p=1时,由 ![]() +
+ ![]() ,解得q=1,舍去.
,解得q=1,舍去.
当2≤p<q时, ![]() ,
, ![]() ﹣
﹣ ![]() =
= ![]() .
.
当3≤p时, ![]() ≥
≥ ![]() ,
, ![]() >0,∴
>0,∴ ![]() +
+ ![]() ,(*)不成立.
,(*)不成立.
∴p=2,可得: ![]() =
= ![]() +
+ ![]() ,解得q=3.
,解得q=3.
∴p+q=5.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系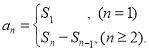 ).
).

练习册系列答案
相关题目
