题目内容
如图,点 是椭圆
是椭圆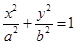 (
(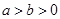 )的左焦点,点
)的左焦点,点 ,
, 分别是椭圆的左顶点和上顶点,椭圆的离心率为
分别是椭圆的左顶点和上顶点,椭圆的离心率为 ,点
,点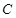 在
在 轴上,且
轴上,且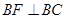 ,过点
,过点 作斜率为
作斜率为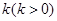 的直线
的直线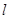 与由三点
与由三点 ,
, ,
, 确定的圆
确定的圆 相交于
相交于 ,
, 两点,满足
两点,满足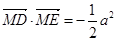 .
.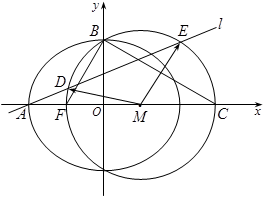
(1)若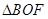 的面积为
的面积为 ,求椭圆的方程;
,求椭圆的方程;
(2)直线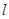 的斜率是否为定值?证明你的结论.
的斜率是否为定值?证明你的结论.
(1)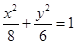
(2)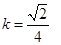
解析试题分析:解:(1)由已知可得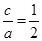 ,
,  , 2分
, 2分
又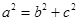 ,
,
解得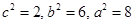 . 3分
. 3分
所求椭圆方程为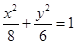 . 4分
. 4分
(2)由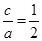 得
得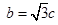 ,则
,则 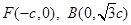 5分
5分
因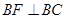 则
则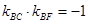 (斜率显然存在且不为零) 6分
(斜率显然存在且不为零) 6分
而 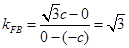
设 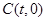 ,则
,则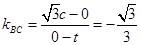
得 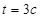 ,所以
,所以 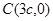 7分
7分
则圆心 的坐标为
的坐标为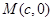 ,半径为
,半径为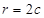 8分
8分
据题意 直线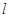 的方程可设为
的方程可设为 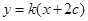 ,即
,即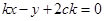 9分
9分
由 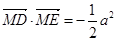 得
得 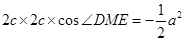 10分
10分
即 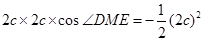 ,得
,得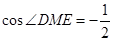 ,而
,而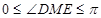
所以 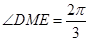 11分
11分
在等腰三角形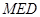 中 由垂径定理可得点
中 由垂径定理可得点 到直线
到直线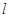 的距离为
的距离为 . 12分
. 12分
则 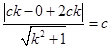 13分
13分
解得 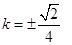 而
而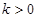 故
故 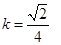 (定值) 14分
(定值) 14分
考点:直线与椭圆的位置关系
点评:主要是考查了直线与椭圆的位置关系的运用,属于中档题。

练习册系列答案
相关题目
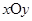 中,经过点
中,经过点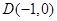 的动直线
的动直线 ,与椭圆
,与椭圆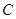 :
: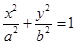 (
( )相交于
)相交于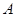 ,
,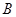 两点. 当
两点. 当 轴时,
轴时,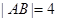 ,当
,当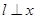 轴时,
轴时,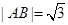 .
. 的中点为
的中点为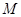 ,且
,且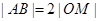 ,求直线
,求直线 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上. 和椭圆
和椭圆 的标准方程;
的标准方程; 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 ,则
,则
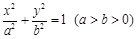 ,其离心率为
,其离心率为 ,经过椭圆焦点且垂直于长轴的弦长为3.
,经过椭圆焦点且垂直于长轴的弦长为3. 与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足
与椭圆C交于A、B两点,P为椭圆上的点,O为坐标原点,且满足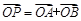 ,求
,求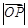 的取值范围.
的取值范围.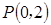 的直线
的直线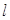 与抛物线
与抛物线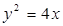 交于
交于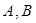 两点,
两点,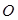 为坐标原点.
为坐标原点.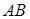 为直径的圆经过原点
为直径的圆经过原点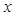 轴于点
轴于点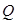 ,求
,求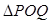 面积的取值范围.
面积的取值范围. -6x+1与坐标轴的交点都在圆C上.
-6x+1与坐标轴的交点都在圆C上.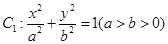 与直线
与直线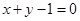 相交于
相交于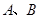 两点.
两点.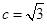 ,直线
,直线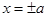 与
与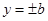 围成的矩形
围成的矩形 的面积为8,
的面积为8,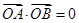 (
(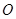 为坐标原点),求证:
为坐标原点),求证: ;
;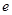 满足
满足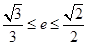 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.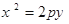
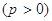 的焦点,A、B、C为该抛物线上三点,已知
的焦点,A、B、C为该抛物线上三点,已知 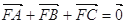 且
且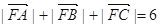 .
.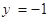 相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。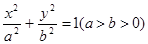 的左焦点为
的左焦点为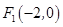 ,直线
,直线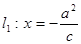 与
与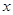 轴交于点
轴交于点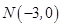 ,过点
,过点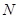 且倾斜角为30°的直线
且倾斜角为30°的直线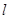 交椭圆于
交椭圆于 两点.
两点. 在以线段
在以线段 为直径的圆上;
为直径的圆上;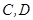 ,以
,以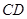 为直径且过点
为直径且过点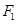 的所有圆中,求面积最小的圆的半径长.
的所有圆中,求面积最小的圆的半径长.